Transmission line circuit for mismatched load and generator

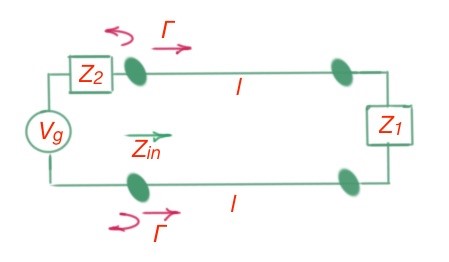
Let’s consider the most general case of a circuit, where we have the arbitrary loads Z_1, Z₂ and an arbitrary generator.

The input impedance of the terminated transmission line is $Z_{i}n=Z_0\frac{e^j\beta l+{\Gamma }_l{e}^{(–j\beta l})}{e^j\beta l–{\Gamma }_l{e}^{(–j\beta l}} ,{\Gamma }_l=\frac{Z_1–Z_0}{Z_1+Z_0}$. The voltage on the line $V\left(z\right)=V_0(e^{–j\beta z}+{\Gamma }_l{e}^{–j\beta z})$ . To receive the voltage of the generator we must take into consideration $z=–l, so V_0=\frac{Z_0{V}_g}{Z_0+Z_2} \frac{e^{–j\beta l}}{1–{\Gamma }_l{\Gamma }_g{e}^{–2j\beta l}}. {\Gamma }_g=\frac{Z_2–Z_0}{Z_2+Z_0}$ is the reflection coefficient of the generator. The standing wave ratio here is $SWR=\frac{1+\left|{\Gamma }_L\right|}{1–\left|{\Gamma }_L\right|}$ . So the power delivered to the load is: $P=\frac{1}{2}\left|V_{i}n{I}_{in}\right|=\frac{1}{2}|V_g{|}^2 \frac{R_{in}}{(R_{in}+R_2{)}^2+(Z_{in}+2{)}^2}$ where $Z_{in}=R_{in}+j{Z}_{in},Z_2=R_2+j{Z}_2$.

1. When the load is matched to the line, $Z_{in}=Z_0,{Г}_l=0$ and $P=\frac{1}{2}|V_g{|}^{2 } \frac{Z_0}{(Z_0+R_2{)}^2+X_2^2}$ .

2. When the load is matched to the line, $Z_{in}=Z_2$ the load power is $P=\frac{1}{2}|V_g{|}^2 \frac{R_2}{4} \frac{1}{(R_2^2+X_2^2)}.$

3. Assuming that the generator impedance is fixed, the condition $\frac{dP}{d{Z}_{in}}\to 0$ leads to the maximum power delivered to the load.

The conjugate matching condition is $R_{(in}=R_g,X_{in}=–X_g,or Z_{in}=Z_g^{*}$ . This condition is conjugate matching, that leads to the maximum power delivered to the load for a fixed generator impedance $P=\frac{1}{2}|V_g{|}^2 \frac{1}{4R_g}$. Figure 1 depicts the general case of transmission line circuit for mismatched load and the generator.

Transmission line with losses