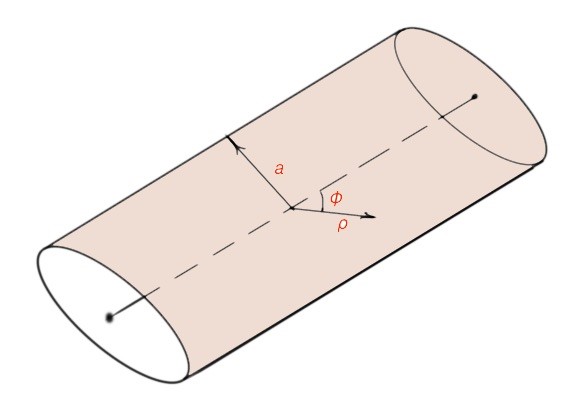
A circular waveguide is schematically depicted in Figure 5. To consider its parameters we will employ the polar coordinates with radial components ρ and angle φ.
So the corresponding electric and magnetic field components for the general case are
Let’s consider the TE waves, where . Considering the and applying the Laplace equation, we can get the magnetic field structure and the rest of the parameters of the waveguide, in a similar way we did before.
So , here and are Bessel functions. The characteristics of the waveguide will be determined by the Bessel function roots pnm. So the parameters of the TE mode transmission line are:
Cut-off wave number .
Propagation constant .
Cut-off wavelength .
Phase velocity .
Dielectric attenuation constant .
Impedance .
For the TM mode of the transmission line, applying the considerations and calculation above we can get the following results:
Cut-off wave number .
Propagation constant .
Cut-off wavelength .
Phase velocity .
Dielectric attenuation constant .
Impedance .
The cut-off frequency for the waveguide can be obtained using the cut-off wavelength. The roots for Bessel functions can be found in mathematic catalogues.