A schematic coaxial transmission line is depicted below and widely used both commercially and industrially, especially in connectors.
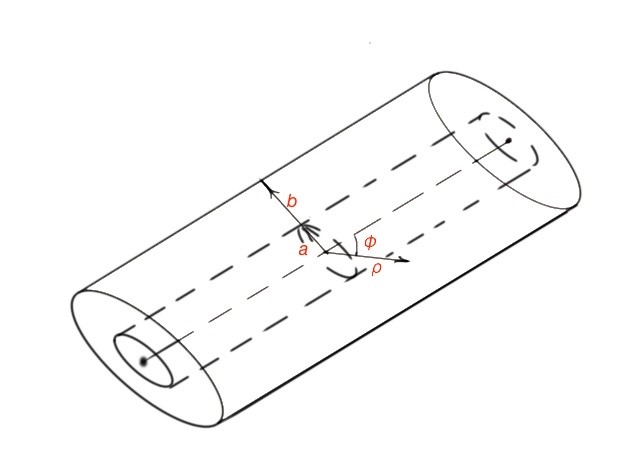
To obtain the field solution for a coaxial transmission line we have to resolve the Laplace equation for potential with the boundary conditions . The easiest way to do this is to use polar coordinates similar to the ones used in a circular waveguide.
The potential function for a given type of coaxial waveguide is . A coaxial line can perform TEM, TE and TM modes. However, in practice the TEM mode is the most common used mode.
Let’s consider the TE mode with , so we must resolve the Laplace equation for . The solution for will be the following: , where and are Bessel functions. The type of electric field function can be obtained using the boundary conditions. The cut-off number here will be .
The transmission line of parallel planes, stripes and microstripes