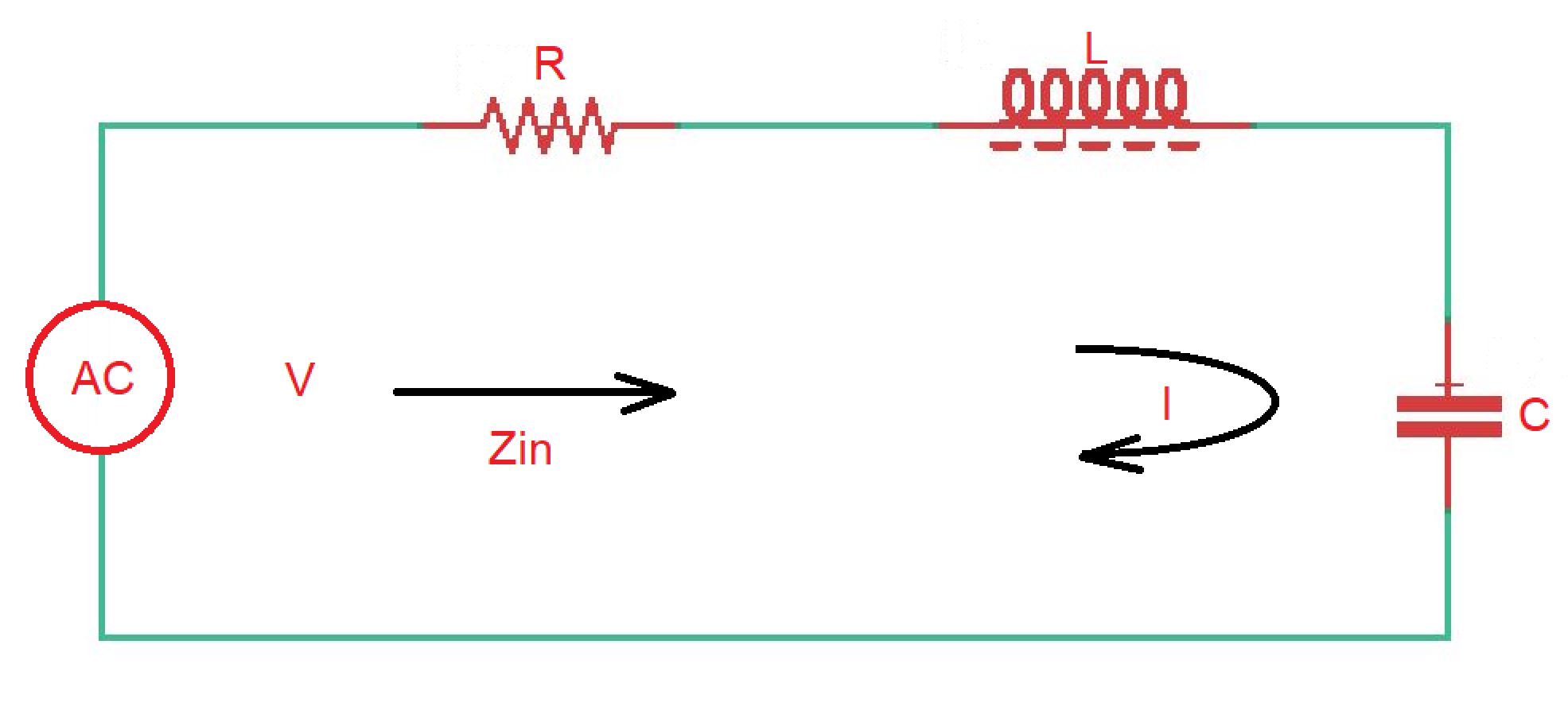
Series RLC resonant circuit

Series RLC resonant circuit is used to model a resonator at frequencies close to resonance. Resonator is a system, demonstrating resonance behaviour. Resonance in a circuit occurs when power stored in the inductor is equal to power stored in capacitor.

Example of this circuit is shown below.

Here input impedance $Z_{in}=R+j\omega L–j\frac{1}{\omega C}$and power delivered to resonator is  $P_{in}=\frac{V{I}^{*}}{2}=\frac{{\left|I\right|}^2}{2}(R+j\omega L–\frac{j}{\omega C})$.

Power dissipated on the resistor $R$ is $P_R=\frac{1}{2}{\left|I\right|}^{2}R$. Magnetic energy stored at the inductor $L$ is $P_L=\frac{1}{4}{\left|I\right|}^{2}L$. Electric energy stored at the capacitor $C$ is $P_C=\frac{1}{4}{\left|I\right|}^2\frac{1}{{\omega }^{2}C}$.

So total power  for this circuit is $P_{tot}=P_R+2j\omega (P_L–P_C)$. At the same time $P_{tot}=\frac{{\left|I\right|}^2{Z}_{in}}{2}$. Here we can get the input impedance as $Z_{in}=\frac{2}{{\left|I\right|}^2}(P_R+2j\omega (P_L+P_C\left)\right)$.

The condition of resonance is equality of energies stored at capacitor and inductor. So $Z_{in}=R$, and input impedance is equal to resistance $R$. And ${\omega }_0=\frac{1}{\sqrt{LC}}$ because $P_C=P_L$.

Resonant circuit is characterised with the quality factor $Q=\omega \frac{P_c+P_L}{P_R}$, which is always proportional to the energy stored in a circuit and energy lost in a circuit.

The reasons of losses in a circuit can be :

• conduction losses;
• dielectric losses;
• radiation losses;
• external circuit losses.

If resonator does not have external circuit, it is called unloaded, and it’s quality factor is $Q_0$. In the other case resonator circuit is loaded and quality factor is $Q$.

In case of unloaded resonant circuit easy to show that $Q_0=\frac{{\omega }_{0}L}{R}=\frac{1}{{\omega }_{0}RC}$.

Let’s consider input impedance in the area of resonance ${\omega }_0+∆\omega$, where $∆\omega \ll {\omega }_0$: $Z_{in}=R+j\omega L(1–\frac{1}{{\omega }^{2}LC})=R+j\omega L(1–\frac{{{\omega }_0}^2}{{\omega }^2})$, where ${\omega }_0=\frac{1}{LC}$.

Mathematically we can show that ${\omega }^2–{{\omega }_0}^2\approx 2\omega ∆\omega$, so $Z_{in}\approx R+j\frac{2R{Q}_0∆\omega }{{\omega }_0}$.