Fields in transmission lines

Let’s consider the general case of electromagnetic waves propagation in transmission lines. Transmission lines can be cylindrical with a parallel core, or can be cylindrical without a core. They can also be empty, contain an insulator or have a conductor inside.

The Maxwell equation for the transmission line is: $\overline{\nabla }\times \overline{E}=-\mathrm{jw\mu }\overline{H}, \overline{\nabla } \times \overline{H}=\mathrm{jw\epsilon }\overline{E}$. The electromagnetic waves spaced in three dimensions are$\overline{E(x,y,z)} =\overline{\left(E\right(x,y)} +\overline{z}{E}_z(x,y)e^{–\mathrm{j\beta z}} ,\overline{H(x,y,z)} = \overline{H(x,y)} +\overline{z}{H}_z(x,y))e^{–\mathrm{j\beta z}}.$ If we derive the expressions for the fields in the Maxwell equation, we can obtain the radial components of the waves $E_x,E_y,H_x,H_y \mathrm{as} a \mathrm{function} \mathrm{of} E_z \mathrm{and} H_z$.

The radial components are $$\begin{gathered} H_x=\frac{j}{k_{c^2}} (\mathrm{w\epsilon }\frac{\partial E_z}{\partial y}–\beta \frac{\partial H_z}{\partial x}),H_y=-\frac{j}{k_{c^2 }} (\mathrm{w\epsilon }\frac{\partial E_z}{\partial x}+\beta \frac{\partial H_z)}{\partial y}), \\ {E}_x=-\frac{j}{k_{c^2}} (\mathrm{w\epsilon } \frac{\partial E_z}{\partial y}+\beta \frac{\partial H_z}{\partial x}),E_y=\frac{j}{k_{c^2}}(\mathrm{w\epsilon }\frac{\partial E_z}{\partial x}–\beta \frac{\partial H_z}{\partial y}) \end{gathered}$$

The transverse electromagnetic waves (TEM) are: $H_z=E_z=0$. Here $\beta =k=w\sqrt{\mathrm{\mu \epsilon }}$ we can also find the fields from the transverse fields equation ${\nabla }^2\mathrm{E(}x,y)=0$ and ${\nabla }^2\mathrm{H(}x,y)=0$. The TEM fields in the transmission lines are the same as the static electromagnetic fields between the conductors.

TEM waves are the electromagnetic waves that are restricted in certain directions. And they can help to resolve the Laplace equation ${\nabla }^2\mathrm{Ф(}x,y)=0$. The voltage can be estimated like a potential difference between two conductors $V={Ф}_2–{Ф}_1,I=\oint \mathrm{Hdl}$. The ratio of transverse fields will tell us the wave impedance for TEM $Z_{\mathrm{TEM}}=\frac{H_x}{E_y}=\sqrt{\frac{\mu }{\epsilon }}$. Thus $\overline{H(x,y)}=\frac{1}{Z_{\mathrm{TEM}}} [e_z,\overline{E(x,y) }]$. TEM waves also exist between three and more conductors.

For transverse electric waves (TE), Hz≠0, Ez=0. The x and y components of the magnetic and electric fields can be obtained from the equations here. The constant β depends on the geometry of the waveguide and the wave frequency. The propagation constant can be determined from the Helmholz equation of the second order. The impedance of the transverse electric wave is $Z_{\mathrm{TE}}=\frac{E_x}{H_y}=\frac{\mathrm{w\mu }}{\beta }$.

For transverse magnetic (TM) waves $H_z=0,E_z\ne 0$. Then the x and y components of the magnetic and electric fields can be found from the equations above. And $Z_{\mathrm{TM}}=\frac{E_z}{H_y}=\frac{\beta }{\mathrm{w\epsilon }}$.

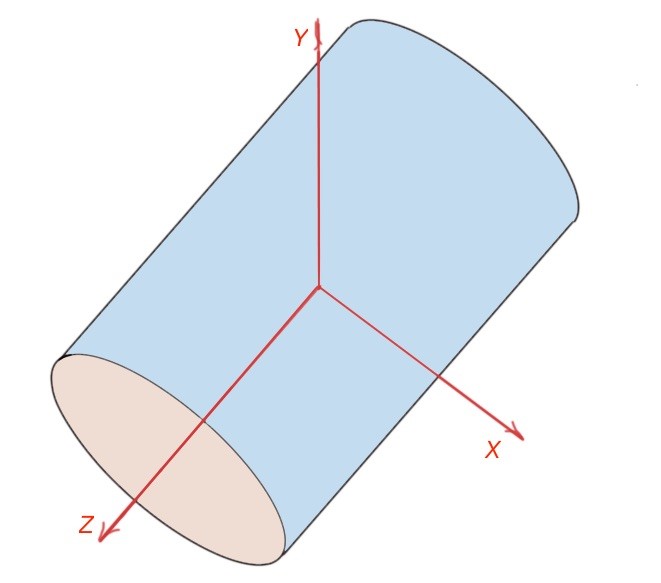
Figure 1. The schematic example of the transmission line.
The attenuation constant for TEM waves is $\alpha =\frac{\mathrm{ktan\delta }}{2},\mathrm{\alpha =}\frac{k^2\mathrm{tan\delta }}{2\beta }$.

Rectangular waveguide