This post answers the question “How do you calculate capacitors in series and parallel?”.
Let’s consider first the series combinaton of two capacitors like on the figure below.
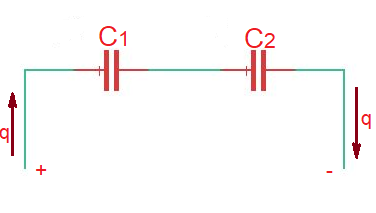
The charge these two capacitors are storing is . At the same time , then or .
For the parallel connection of capacitors like on the figure below, we can conclude that and .
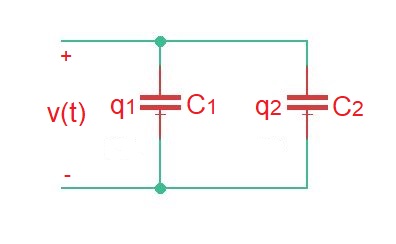
Then . And . Then .
More educational content can be found at Reddit community r/ElectronicsEasy.