What is inductor and how does it work

This post answers the question: “What is inductor and how does it work?”. Here we consider the inductance concept and it’s main feature. As soon as we are considering not only effective capacitors and inductors in the circuit, but also parasitic capacitances and inductances, it is important to consider how these effects work.

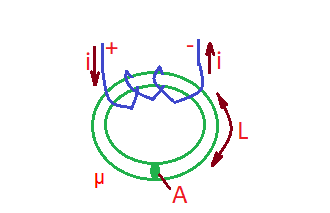
Inductor in the circuit models the effect of magnetic fields, like capacitor – electric fields. Let’s consider the ideal two-terminal inductor. Here we have N  coil turns around the inductor core with permeability $\mu$. Core length is $l$, and cross-section area is $A$. Current $i\left(t\right)$ through the coil creates magnetic flux in the inductor with density $B\left(t\right)=\frac{N\mu i\left(t\right)}{l\left(t\right)}$, so magnetic flux through the core of the inductor is $\Phi \left(t\right)=B\left(t\right)A\left(t\right)$. As soon as there is $N$ coil turns, we are getting the total flux through the inductor $\lambda \left(t\right)=\frac{\mu N^{2}A\left(t\right)i\left(t\right)}{l\left(t\right)}$. As soon as total flux through the inductor is the inductance through the inductor multiplied with the electric current, then the inductance of the inductor $L\left(t\right)=\frac{N^2\mu A\left(t\right)}{l\left(t\right)}$, inductance is measured in Henry (H) or Webers/Ampere.

From Maxwell’s equations we know that $\frac{d\lambda \left(t\right)}{dt}=v\left(t\right)=L\left(t\right)\frac{di\left(t\right)}{dt}$.

From here we can get $i\left(t\right)=\frac{1}{L}{\int }_{–\infty }^{t}v\left(t\right)dt$.

Same as in case with capacitor, inductor also has memory feature of branch voltage.

Here we can find that $\frac{d{\omega }_M\left(t\right)}{dt}=i\left(t\right)v\left(t\right)$ and $d{\omega }_M=id\lambda$. It means that stored energy in the inductor is ${\omega }_M\left(t\right)=\frac{{\lambda }^2\left(t\right)}{2L}=\frac{L{i}^2\left(t\right)}{2}$.

Educational content can also be reached via Reddit community r/ElectronicsEasy.