This post answers the question: “How do you calculate inductors in series and parallel?”.
Let’s consider series connection of two inductors depicted below.
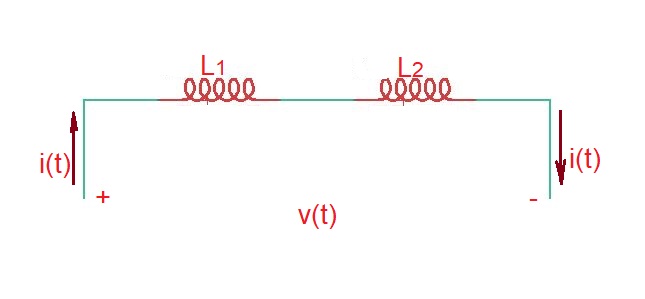
Current through each conductor in the series connection , the total flux here . It means that effective inductance .
Let’s now consider parallel combination of two inductors depicted below.
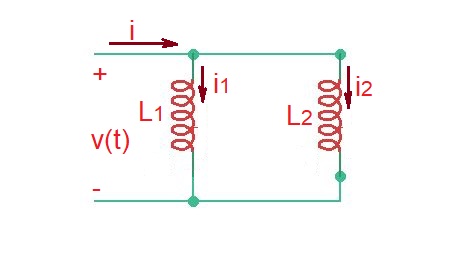
As soon as these inductors have equal voltage we can write that . At the same time . From here we can obtain .
More educational content can be found at Reddit community r/ElectronicsEasy.