Equivalent two-terminal network

Equivalent two-terminal transformations are transformations that lead to the simplification of complex two-terminal networks with the smallest amount of $L, C$and $R$ elements.

These equivalent networks are called canonical networks. The transformations for network simplification are transformations from star to triangle (or vice versa), transformation from parallel-series network to parallel (or vice versa). If the two-terminal networks have equal input resistances with all the frequencies, they are called equivalent networks.

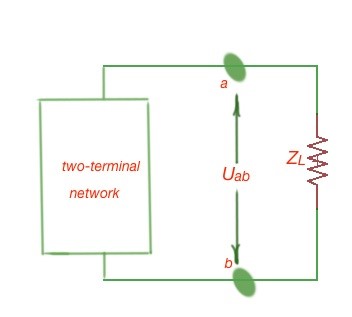
Let’s consider the two-terminal network on the figure below. Here $Z_L=R_L+j{X}_L$, the two-terminal resistance is $Z_{tt}=R_{tt}+j{X}_{tt}$, so the load current is $I=\frac{U_{\mathrm{ab}}}{Z_{\mathrm{tt}}+Z_L}=\frac{U_{\mathrm{ab}}}{R_{\mathrm{tt}}+R_L+j(X_L+X_{\mathrm{tt}})}$. The load power will be at maximum if the $R_L=R_{\mathrm{tt} }\mathrm{and} X_L+X_{\mathrm{tt}}=0$, so in order to get the maximum power on the load the load resistance should be $Z_L=R_{tt}+j{X}_{tt}$.

Usually the load resistivity $Z_L$ is fixed, and to connect this load to the two-terminal device the matching transformer is used. Let’s assume that ${\omega }_1$ and ${\omega }_2$ is the quantity of coils of the primary and secondary coils of the matching transformer. The core of the transformer is made of magnetic material. This transformer is close to the ideal transformer, so we neglect its inductance and active resistance. This network is shown in Figure 2. Here $Z_{\mathrm{in}}=\frac{U_{\mathrm{ab}}}{I}=\frac{U_L{\displaystyle \frac{{\omega }_1}{{\omega }_2}}}{I_L{\displaystyle \frac{{\omega }_2}{{\omega }_1}}} =R_L\frac{{\omega }_{1^2}}{{\omega }_2}+{\mathrm{jX}}_L\frac{{\omega }_{1^2}}{{\omega }_2}$. This resistance should match to the load resistance $Z_{\mathrm{in}}=R_{\mathrm{in}}+{\mathrm{jX}}_{\mathrm{in}},$ then $R_{in}=R_L\frac{{{\omega }_1}^2}{{\omega }_2}, X_{in}=–X_L\frac{{{\omega }_1}^2}{{\omega }_2}$.

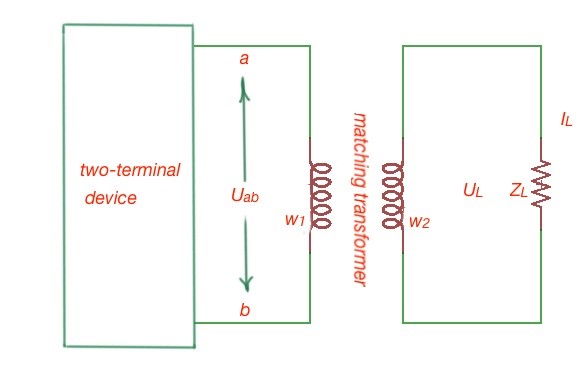
The transformer is called ideal  when its input and output characteristics are related in the following way: $U_1=\frac{{\omega }_1}{{\omega }_2} U_2, I_1=\frac{{\omega }_2}{{\omega }_1} I_2, Z_1=\frac{{\omega }_{1^2}}{{\omega }_2} Z_2.$

Magnetically