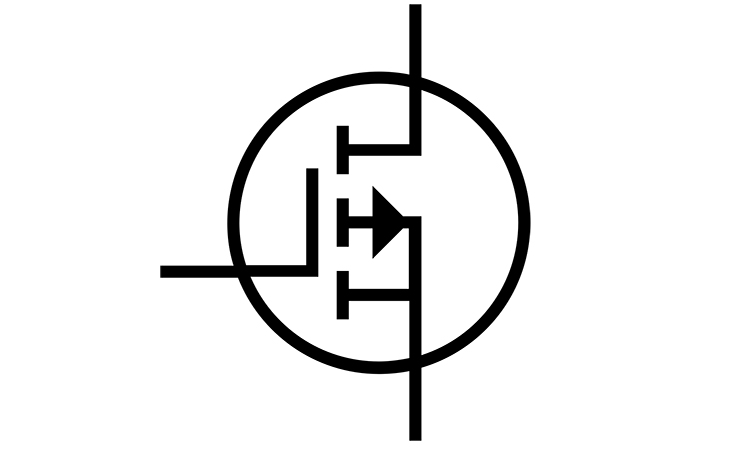
A depletion MOSFET is a one state transistor, that is in an ON state even when the gate to source voltage VGS or VGSS is zero. The gate to source voltage can be marked in two ways depending on the manufacturer.
The depletion MOSFET is structurally the same as an enhanced MOSFET, but the oxide layer of the gate is separated from the substrate by a thin n-type doped layer. So, unlike an enhanced MOSFET, a depletion MOSFET always has a conducting channel. Figure 1 shows the layer structure of a depletion MOSFET, and its circuit sign.
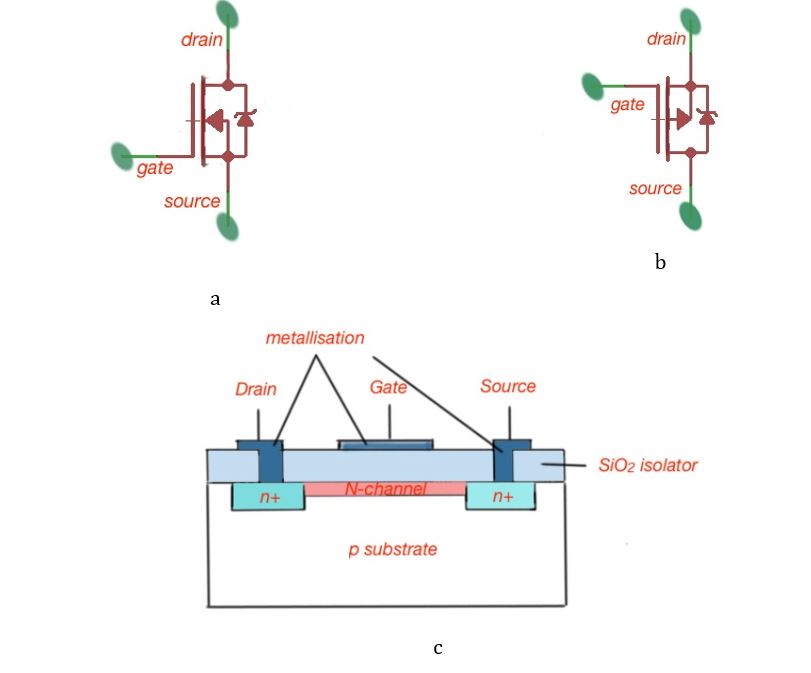
If the VGS increases the resistance of the conducting layer decreases. If the VGSS < 0, then the conducting layer will be depleted in the charge carriers, and the resistance will grow. When VGSS < VT, VT is a threshold voltage that is negative in the depletion MOSFET, then all charge carriers will be repelled into the substrate.
It corresponds to the cut–off region. When the VGSS < VT, the MOSFET is in an ohmnic region and acts as a variable resistor. When the drain-source voltage Vds increases to the value of the gate-source voltage VGS, then the device is in the pinch-off region, and the conducting layer becomes narrower at the drain until it is totally pinched-off. When the pinch-region is reached, the MOSFET occurs in the saturation region. Basically the operation of the depletion MOSFET is the same as an enhanced MOSFET, but with negative VT.
Figure 2 depicts how a depletion MOSFET can be used in the circuit. When voltage at the source is 0V, voltage through the MOSFET and a resistor is 0V. When the voltage VGS is 0V, there will be some current through the MOSFET. When the voltage source applies some voltage through the circuit, the VGS = IDR1. That in turn reduces the VGS
When VGS is negative, the current through the MOSFET decreases. The current . Here IDSS is a current through the transistor – when VGS = 0, VT is a gate threshold voltage of the MOSFET.
The drain-source voltage is When VDS is low, the MOSFET is in resistive mode of operation. When the VDS is high, the MOSFET is in linear mode, where ID gets saturated and does not depend on the VDS, the formula for the ID we stated above is valid. The condition of linear mode is .
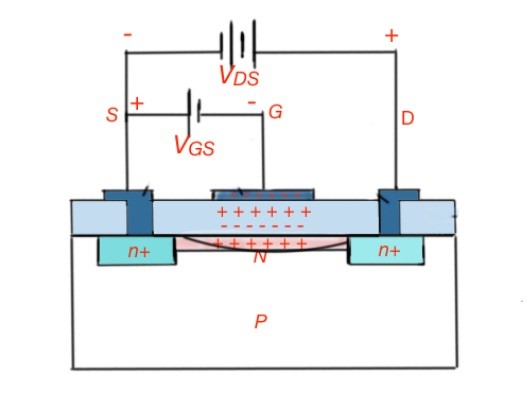
When the MOSFET is in linear mode, in combination with a series resistor, it can be used as a constant current source. The current in linear mode depends on the VGS and the resistance R1. So for the required current, the series resistance can be calculated .
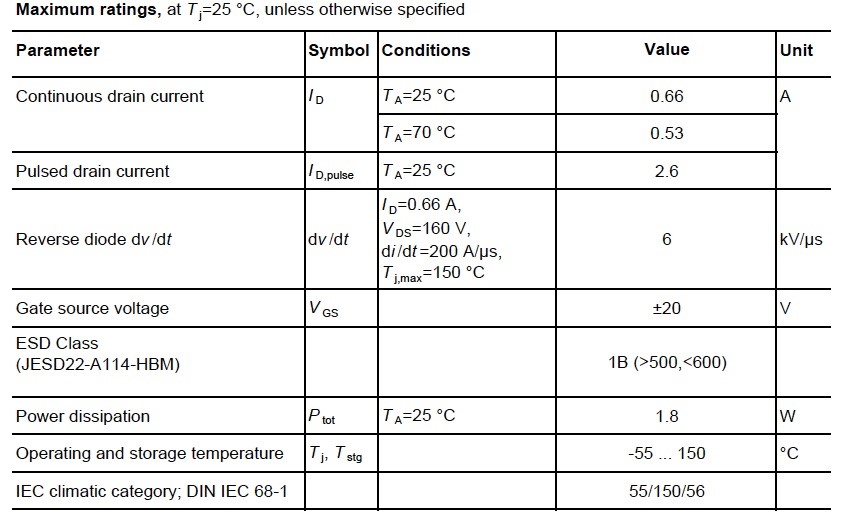
What’s in the MOSFET datasheet? As an example we can consider the depletion MOSFET Infineon BSP149 with the characteristics below in Figure 3. All the symbols are also provided in the datasheet. The first table we see is the maximum ratings. This data is most important when you design a circuit, they are not standardised and vary from manufacturer to manufacturer.
The maximum ratings are calculated data, and not a result of an experiment or testing of the MOSFET. They are related to the circuit condition as a whole structure, it’s thermal characteristics and so on. Maximum ratings can not be exceeded in order to support the device’s normal operation during it’s life-time.
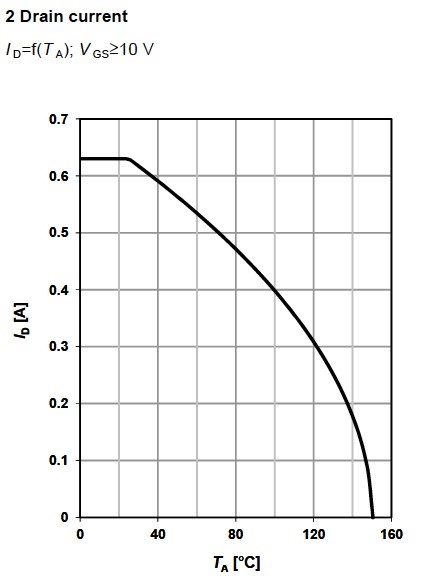
Let’s consider in detail what the consistents are of the Maximum ratings. Drain current, current that can pass through the MOSFET in the forward direction, ID, and pulsed drain current that the MOSFET can pass in the forward direction IDpulse Some manufacturers also mention currents in reverse direction as well. The maximum continuous drain current depends on the power dissipation and is defined by the formula . The datasheet provides the graph for drain current ID(TC).
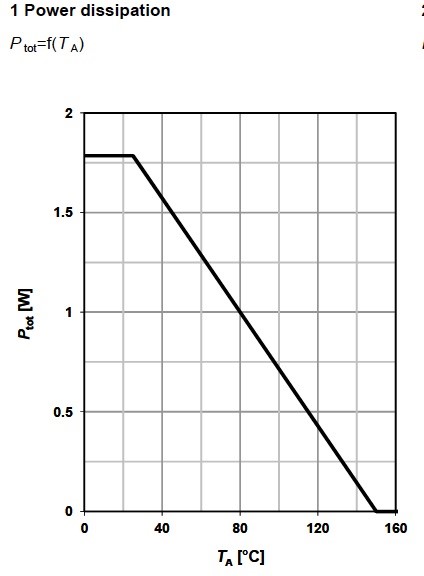
Above we referred to the Power dissipation of the device. The power dissipation graph is depicted in Figure 5 and the power dissipation ratings are also mentioned in the Maximum ratings table – there is two of them – total junction-to-case and total-junction-to-ambient power dissipation. The junction-to-case thermal resistance RthJC depends on the material and dimensions. The junction-to-ambient thermal resistance RthJA depends on the layout. The total power dissipation values can be obtain by the formula .
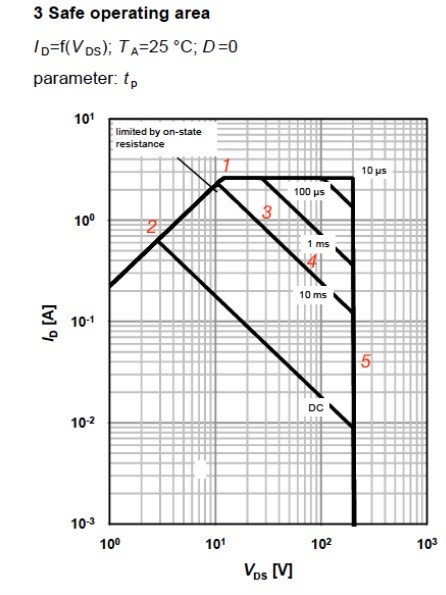
The Safe operation area (SOA) graph (Figure 6) shows the drain current as a function of drain-source voltage with different pulses lengths. This is a very important graph that describes the regions of operation of the MOSFET (we considered above) and also its limits.
Line is a limit of the maximum ID,pulse. Area is limited by an on-state resistance RDS(on) at the maximum junction temperature. Area , when the case temperature TC is fixed, the device is limited by the constant power. Dispensing on the applied power pulse width, the maximum power loss varies according to the thermal impedance.
In Area , in linear mode operation, there is a risk of getting hot spots at low gate-source voltages due to thermal escape. This effect is very important for the latest technologies. For hot spots with high VDS and long pulses SOA is described by the formula: . Region shows the maximum breakdown voltage VBR(DSS) that is determined by technology.
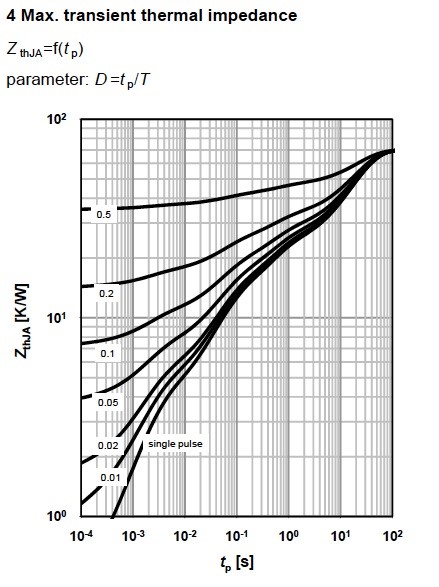
Maximum transient thermal impedance ZthJC. Thermal impedance consists of thermal resistance Rth and thermal capacitance Cth. The transient thermal impedance ZthJC takes into account the thermal resistance from the junction to the die of the case, RthJC ( the power loss in the device), and heat capacity CthJC.
The maximum transient thermal impedance as a function of the loading time tp (or the pulse width) is depicted in the Figure 7. This graph is depicted for different duty cycles . The MOSFET device consists of several layers, and heat passes through all of them (each layer has characteristic resistance and capacitance).
The heat dissipation will depend on the thermal resistances, thermal capacitances and pulse width. The junction temperature can be obtained with the formula , where Tj,start is the TCat the thermal equilibrium.
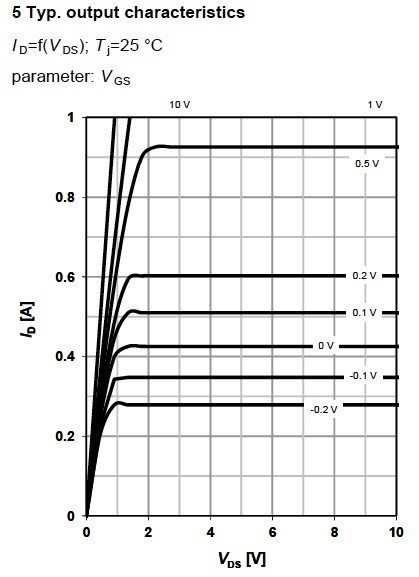
The next graph in the datasheet is Output characteristics, (Figure 8) which describes drain current ID as a function of the drain-source voltage VDS in certain conditions. This graph is depicted for the ohmic region, because MOSFETs operate optimally there.
This graph is divided into two parts – ohmic and saturated regions. The saturated region starts when Operation at the saturation region of the MOSFET is dangerous, because when the ID increases, the VDS increases gradually, which leads to the rise of conduction losses, and the MOSFET may fail. The range of VGS mentioned in the datasheet determines the output characteristics in the graph.
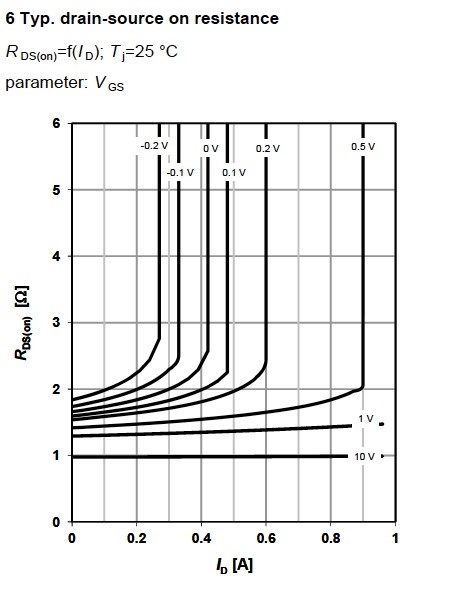
Drain-source on state resistance RDS(on) graphs are next in the datasheet. The drain source on state resistance RDS(on) as a function of drain current ID is calculated from the output characteristic curves, with the formula . This curve changes massively depending on the applied VGS (Figure 9).
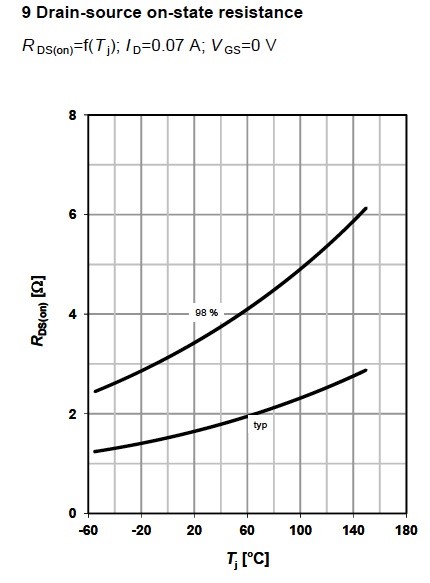
Drain-source on state resistance RDS(on) as a function of junction temperature Tj. Figure 10 shows the typical and maximum values for the resistance, and they are determine after testing during production. The data set for RDS(on) can be calculated by the formula: is a technology constant.
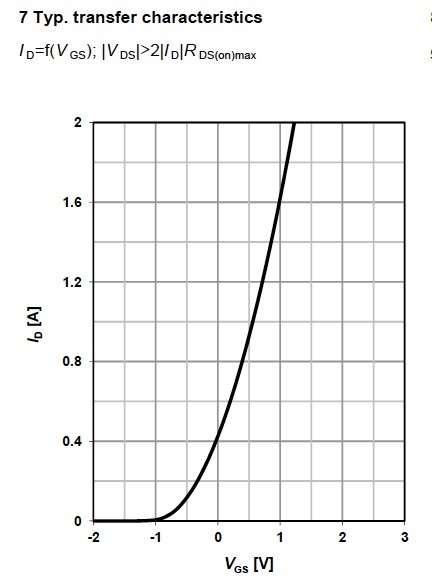
Typical transfer characteristics graph (Figure 11) shows the typical drain current ID as a function of source-gain voltage VGS at different junction temperatures. There can be more than two curves, and all them are intersecting at the point called the temperature stable operating point.
When the VGS is below this point, the MOSFET is characterised by the positive temperature coefficient, then the junction temperature Tj growth leads to the drain current ID rise. The operation with constant VGS may fail the device because of thermal escape. When the VGS is bigger than the operating point value, then the thermal coefficient is negative, and the rise of junction temperature Tj will decrease the drain current ID. The MOSFET operating in this interval should be fine as soon as Tj is within the datasheet limits.
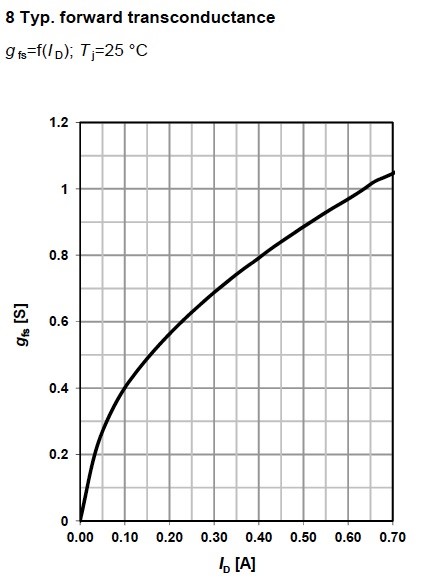
The datasheet shows the Typical forward transconductance (Figure 12), gfs that is the measure of sensitivity of the drain current ID to the deviation of the gate-source voltage VGS. It can be obtained by the formula .
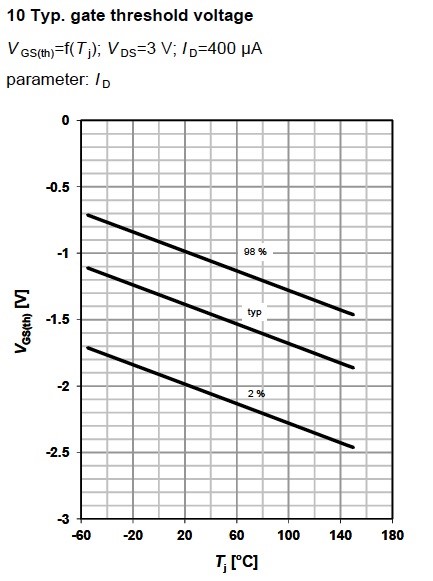
Gate threshold voltage VthGS (Figure 13) shows the required gate-source voltage VGS at specific drain current ID. The threshold voltage is measured during production when VGS = VDS at a specific drain current. This data can be found in the maximum ratings table.
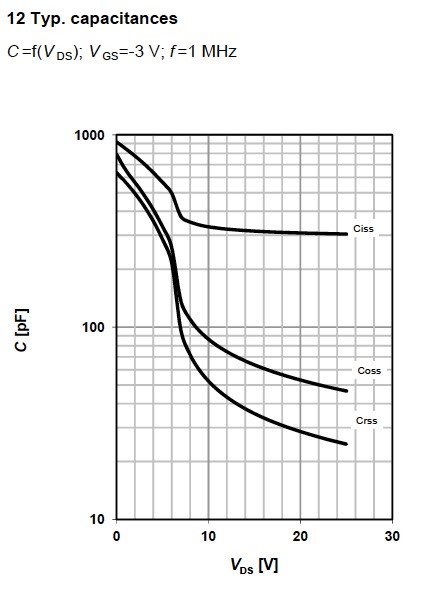
The Dynamic characteristics table shows the Capacitances for the MOSFET – input, output and reverse transfer capacitances. They are described by the formulas: . Figure 14 shows input, output and reverse transfer capacitances are shown as a function VDS.
Here we have considered the most important characteristics from the datasheet, describing the N-type depletion MOSFET. However, the order and the quantity of graphs and data may vary from vendor to vendor.
(Engineering Principles and Applications of Electrical Engineering, 5th edition, G.Rizzoni; BSP149 datasheet, Infineon, www.infineon.com; Infineon OptiMOS MOSFET datasheet explanation, www.infineon.com)