What is a JFET transistor and how it works

This post is about structure, parameters and properties of JFET transistor.

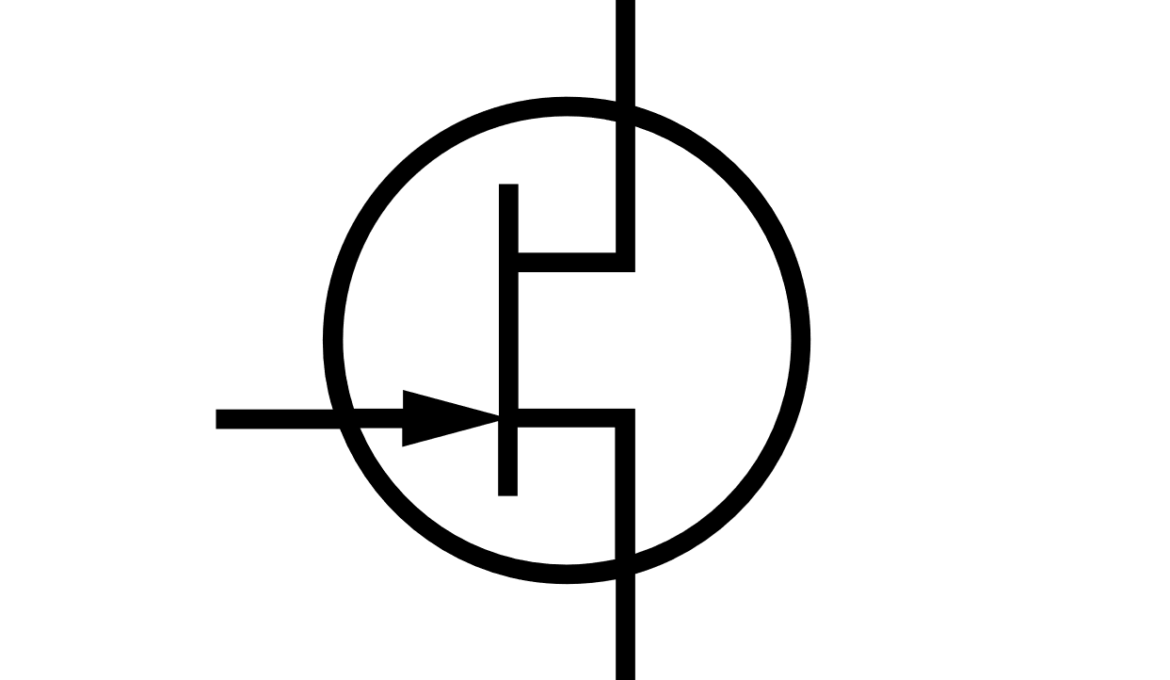
JFET transistor is a three-terminal device, where one of the terminal can control current between two others. JFET transistor terminals are drain (D), source (S) and gate (G). Here current between D and S can be controlled by gate-source voltage.

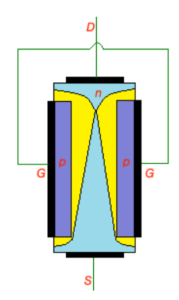
Construction of JFET transistor is depicted on the figure below. N-type JFET transistor consist of n-type semiconductor with heavily doped p-type regions as shown on the figure. P-type areas are forming the gate, both p-type areas and n-type area are equipped with thin contacts layers.

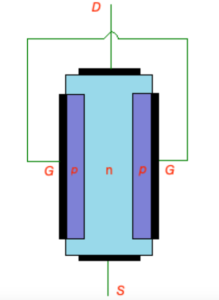
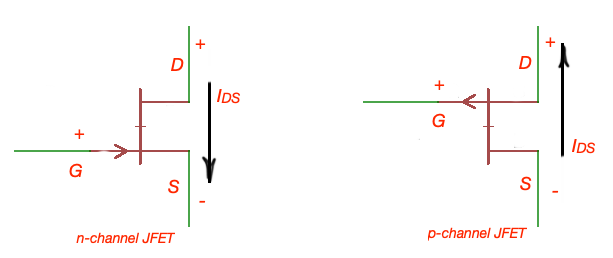
JFET n-type

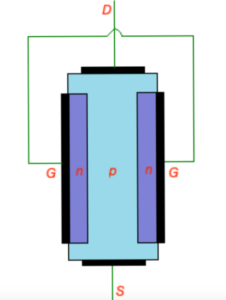
JFET p-type

JFET electrical symbols

Let’s consider n-type JFET transistor. Here n-type semiconductor is connected to drain and source with ohmic contacts, p-type semiconductors are connected to the gate and connected to each other.

JFET transistor is in cut-off mode, and does not conduct any current when both source-gate and drain-source potentials are zero. There is thin depletion regions are formed around p-type regions of JFET. Depletion regions are free from free careers, so there is no current through depletion area.

Let’s keep $v_{G S} = 0$ and apply drain-source voltage $v_{D S} > 0$ . Current $I_{D}$ will flow from drain and source (note that electrons will move in the opposite direction). Here JFET transistor operates in ohmic mode. Depletion region around p-type areas is wider close to drain because of the voltage distribution between drain and source. When $v_{D S}$ is growing, width of depletion areas close of drain is growing as well. At some point drain-source voltage will reach $v_{P}$ level, when these depletion areas will get very close to each other. $v_{P}$ voltage is called pinch-off voltage. After this point JFET transistor will go to the saturation mode. Here small channel between two depletion areas will still exist with constant current through is $I_{D S S}$ .

If $v_{G S} < 0$ , depletion regions still grows around p-type areas of JFET transistor. In order to maintain depletion regions $v_{G S}$ should be smaller than $v_{D S}$ . Lower $v_{G S}$ . lower pinch-off voltage $v_{P}$ . Finally when $v_{G S} = - v_{P}$ , $I_{D S S} = 0$ . JFET is off.

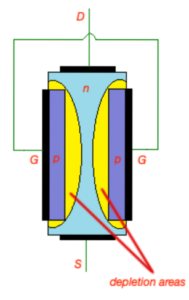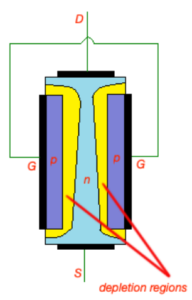Ohmic mode

Saturation mode

When JFET transistor operates in ohmic mode, the resistance of n-channel can be controlled by $v_{G S}$ voltage, so JFET behaves like a voltage-controlled resistor. First approximation of JFET resistance in this case is $r_{D S} = \frac{{v^{2}}_{P}}{2 I_{D S S} (v_{G S} + V_{p})^{2}}$ .

Finally equations, describing JFET transistor behaviour are:

$V_{G S} < - V_{p}$ for cut-off region;

$v_{D S} > V_{b r e a k}$ for breakdown voltage;

$v_{D S} < \frac{v_{G S} + v_{p}}{4}, v_{G S} > - v_{p}$ , $i_{D} = \frac{i_{D S}}{R_{D S}}$ , $R_{D S} = \frac{{v_{p}}^{2}}{2 I_{D s S} (v_{G S} + v_{p})}$ for ohmic region;

$i_{D} = \frac{I_{D S S}}{{v_{p}}^{2}} (v_{G S} + v_{p})^{2}, v_{D S} > v_{G S} + v_{p}, v_{G S} > - v_{p}$ for saturation region. Here $I_{D S S}$ is a maximum current, when $v_{G S} = 0$ and $v_{D S} > v_{P}$ .

If $v_{G S} < v_{P}$ , $I_{D} = 0$ .

If $0 < v_{G S} < v_{P}$ , then $0 < i < I_{D S S}$ .

JFET transistor transfer function

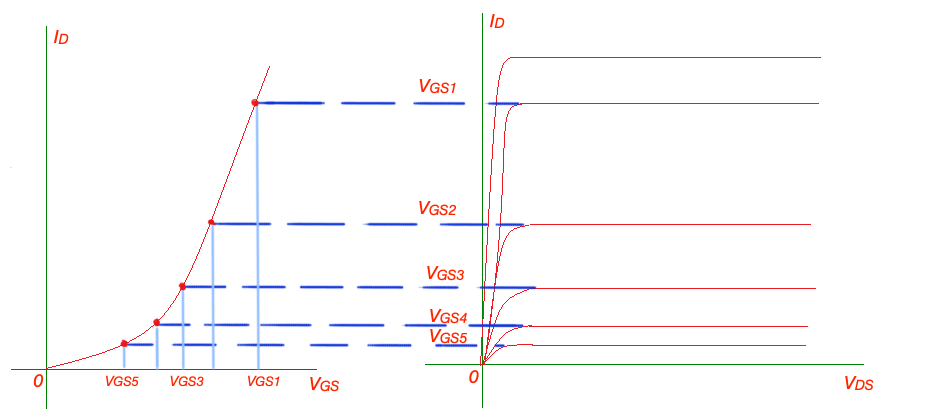
Transfer characteristic is the relation between output current $I_{D}$ and controlling voltage $V_{G S}$ . The easiest way to obtain transfer characteristic is to apply Shockley equation $I_{D} = I_{D S} (1 - \frac{v_{G S}}{v_{P}})^{2} = f (v_{G S})$ . It gives us $I_{D} = I_{D S S,}$ when $v_{G S} = 0$ and $I_{D} = 0$ , when $v_{G S} = v_{p}$ . Here we are having important relationship between $v_{G S}$ and $v_{P}$ is $v_{G S} = v_{P} (1 - \sqrt{\frac{I_{D}}{I_{D S S}}})$ .

In order to outline the transfer function, we must calculate $I_{D}$ current for different key levels of $v_{G S}$ .

Transfer function can be obtained from the $I_{D} (v_{D S})$ characteristics like on the figure below.

Fixed-bias JFET configuration

Three most important relationships for operation of FET transistor devices are $I_{G} = 0, I_{D} = I_{S}$ and Shockley equation $I_{D} = I_{D S S} (\frac{1 - V_{G S}}{v_{P}})^{2}$ .

Here $v_{i n}$ and $v_{o u t}$ are ac levels.

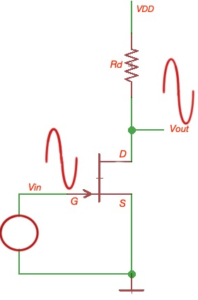
$v_{D S} = v_{D D} - I_{D} R_{D}$ , $v_{G} = v_{G S}$ , $v_{D} = v_{D S}$ , because $v_{S} = 0 V$ .

$I_{D} = I_{D S S} (1 - \frac{v_{G S}}{v_{P}})^{2}$ .

Self-biased JFET transistor configuration

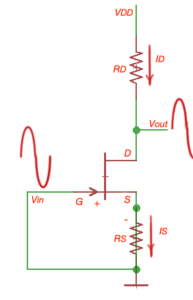
Here $v_{R S} = - v_{G S}$ , and from the other side $v_{R S} = I_{S} R_{S}$ , $I_{D} = I_{S}$ then $v_{G S} = - I_{D} R_{S}$ and $v_{D S} = v_{D D} - I_{D} R_{S} - I_{D} R_{D}$ . $v_{G} = 0, v_{S} = I_{D} R_{S}, a n d v_{D} = V_{D D} + I_{D} R_{S}$ ,

In accordance to Shockley equation $I_{D} = I_{D S S} (1 + \frac{I_{D} R_{S}}{v_{P}})^{2}$ , then we are having second order equation that will lead us to quadratic function.