Electromagnetic induction occurs in different ways. For example, when current changes in the circuit, there is different kinds of EMF that occurs in the conductor – one of them is self-induction EMF ԑsi, and additional currents Iα.
When the current in a circuit changes, the magnetic flow through the surface enclosed by the circuit changes, and leads to self-induction EMF in the circuit:
The change of every fragment of magnetic flux in the circuit is proportional to the magnetic field in this point. At the same time, by the Biot-Savart-Laplace Law, it’s proportional to the current in a circuit. So we can conclude that Ф~I. Technically, Фs = LI where L is the self-induction coefficient – that is ratio of the self-induction magnetic-flux through the circuit to the current of the circuit.
Magnetic properties of the circuit affect the inductance. Here we can introduce the term of magnetic permittivity – that is the ratio of inductance of the circuit element in the substance, and inductance in the vacuum.
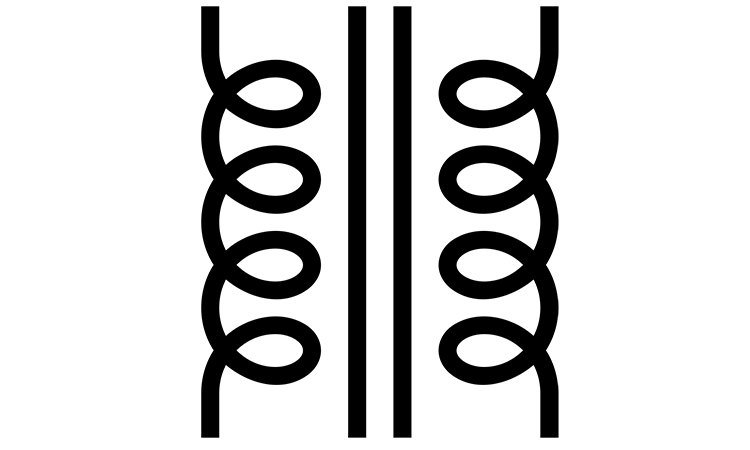
Solenoid inductance
In accordance to the formulas above, the self-induction EMF is
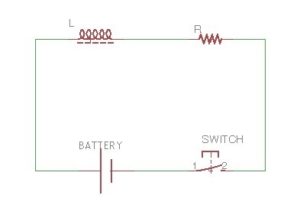
If two circuits are placed close to each other, the current in the first circuit creates magnetic flux through the second circuit, and the current in the second circuit creates magnetic flux through the first circuit. Ф2 = L12I1, Ф1 = L21I2. In this case we can talk about the term of mutual inductance. L12 and L21 are the mutual inductance coefficients, and they depend on the geometry of inductance, and its properties. When ferromagnetics are absent in the system L12 = L21. Self-inductance is closely related to the transition processes in the circuit – the processes of establishment and relaxation of the current in the electric circuit. And these processes feature some delays. Let’s consider the circuit C on the Figure 33. In accordance to the Kirchhof’s Law
Mathematical transitions will lead to the following formula:
We must take an integral of both sides of these equations:
And
where
– is a time coefficient for the circuit.