We will cover the topic of dielectrics in the Electronic Materials chapter in detail. Here is a brief explanation of the main terms about dielectrics. Dielectrics are materials that do not conduct electric current, because they do not contain free charges.
However, there are charged particles that can be bonded in a molecule – bonded charges. In the electric field these bonded charges can shift distance up to 10-9m. As a result the dielectric polarises. And its summarised dipole moment is
There are several types of polarisation in dielectrics.
Dipole polarisation
Dipole polarisation is a characteristic of substances that already contain dipole molecules, which are chaoticly oriented when the electric field is 0.
Electron polarisation
This type of polarisation is a characteristic of the molecules, that obtain dipole moment only in the electric field, because of the shift of electron density in molecules.
Polarisation is characterised by the vector of polarisation , is an element of matter characterised by the vector and polarisation vector . Polarisation vector is proportional to the electric field, , is dielectric susceptibility.
What is the electric field in the dielectric? It consists of the electric field of bonded charges and free charges (surface charges).
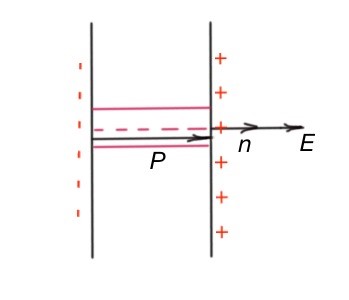
this electric field is an average, because electric field changes significantly, close to an atom’s nuclei. Polarisation vector P may help to recognise polarised charges. Let’s consider a thin layer of dielectric between capacitor plates, Figure 26. -11.8., where the electric field E is constant. Bonded charges of this layer are +σ and –σ. The dipole moment of this thin layer is
also
then
and