Transient Response of RL Circuit

After the introduction of the SMU ADALM1000 let’s continue with the fifth part of our series with some small, basic measurements.

By Doug Mercer and Antoniu Miclaus, Analog Devices

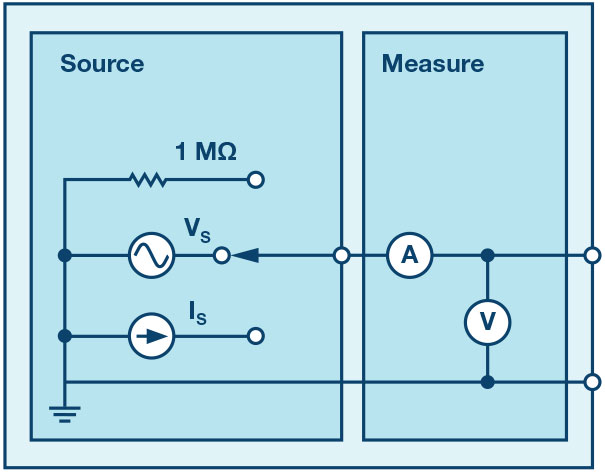
Now let’s get started with the next experiment.

Objective:

The objective of this lab activity is to study the transient response of a series RL circuit and understand the time constant concept using pulse waveforms.

Background:

This lab activity is similar to another of our lab activities, Activity 4: Transient Response of an RC Circuit, except that the capacitor is replaced by an inductor. In this experiment, you will apply a square waveform to the RL circuit to analyze the transient response of the circuit. The pulse width relative to the circuit’s time constant determines how it is affected by the RL circuit.

Time Constant ( $τ$ ): A measure of time required for certain changes in voltages and currents in RC and RL circuits. Generally, when the elapsed time exceeds five time constants ( $5 τ$ ) after switching has occurred, the currents and voltages have reached their final value, which is also called the steady-state response.

The time constant of an RL circuit is the equivalent inductance divided by the Thévenin resistance as viewed from the terminals of the equivalent inductor.

τ = \frac{L}{R}

A pulse is a voltage or current that changes from one level to another and back again. If a waveform’s high time equals its low time, it is called a square wave. The length of each cycle of a pulse train is its period ( $T$ ). The pulse width ( $t_{p}$ ) of an ideal square wave is equal to half the time period.

The relation between pulse width and frequency for the square wave is given by: $f = \frac{1}{2 t_{p}}$ .

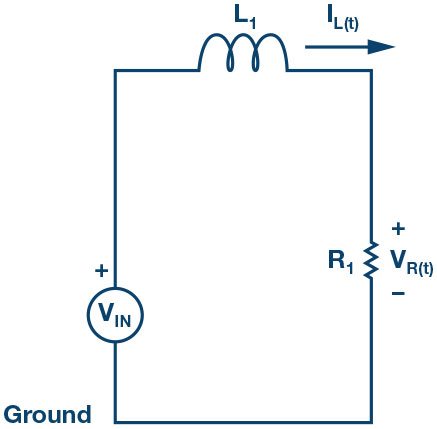
In an RL circuit, voltage across the inductor decreases with time, while in the RC circuit, the voltage across the capacitor increased with time. Thus, current in an RL circuit has the same form as voltage in an RC circuit: they both rise to their final value exponentially according to $1 - e^{- t \frac{R}{L}}$ .

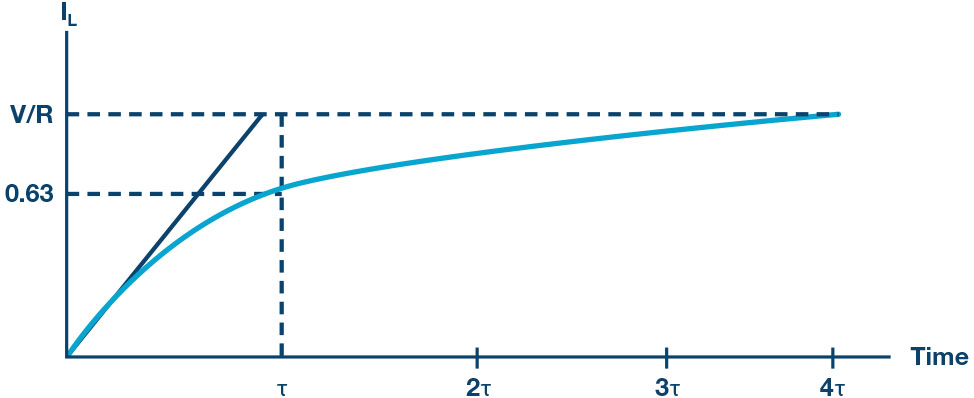
The expression for the current in the inductor is given by: $I_{L} (t) = (\frac{V}{R}) (1 - e^{- t \frac{R}{L}}), t \geq 0$ , where $V$ is the applied source voltage to the circuit for $t = 0$ . The response curve increases and is shown in Figure 3.

Figure 3. The current in an inductor increasing in a series RL circuit.

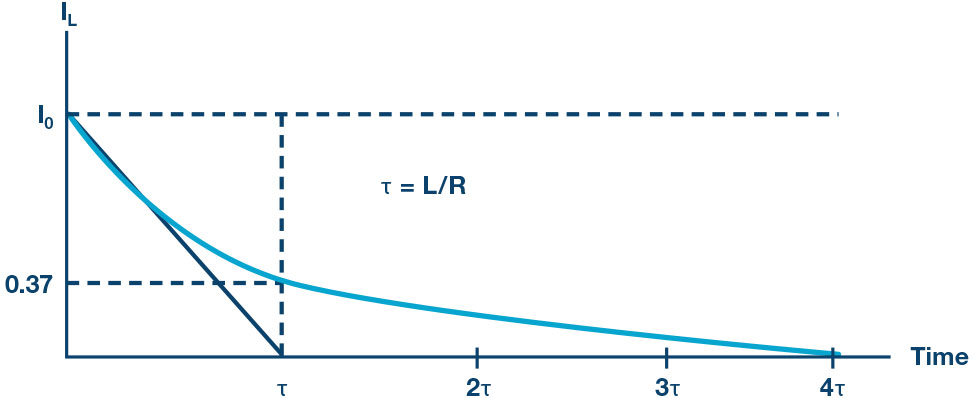
The expression for the current decay across the inductor is given by: $I_{L} (t) = I_{0} e^{- t \frac{R}{L}}, t \geq 0$ , where

I_{0}

is the initial current stored in the inductor at

t = 0, τ = \frac{L}{R}

is the time constant. The response curve is a decaying exponential and is shown in Figure 4.

Figure 4. The current decay through the inductor for a series RL circuit.

Since it is possible to directly measure the current through the inductor (current supplied by driving source) with the ALM1000, we will measure and compare both the current and the output voltage across the resistor. The resistor waveform should be similar to the inductor current as $V_{R} = I L_{R}$ . From the waveforms on the scope, we should be able to measure the time constant τ, which should be equal to $τ = \frac{L}{R_{t o t a l}}$ .

Here, $R_{t o t a l}$ is the total resistance and can be calculated from $R_{t o t a l} = R$ inductance $+ R$ .

R inductance is the measured value of inductor resistance and can be measured by connecting inductance to an ohmmeter prior to running the experiment.

Materials:

ADALM1000 hardware module
One resistor (220 Ω)
One inductor (20 mH (two 10 mH in series))

Procedure:

Measure the combined inductor and resistor resistance $R_{t o t a l}$ by using an You can use the ALM1000 ohmmeter tool to do this. Remember that the ohmmeter tool measures resistance with respect to ground when you connect the series connected $L 1$ and $R 1$ .
Set up the circuit shown in Figure 5 on your solderless breadboard with the component values R1 = 220 Ω and L1 = 20 Open the ALICE oscilloscope software.

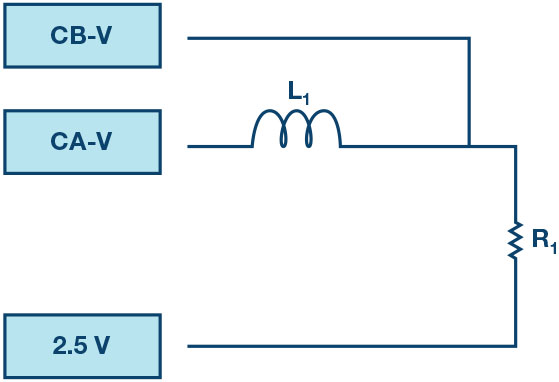
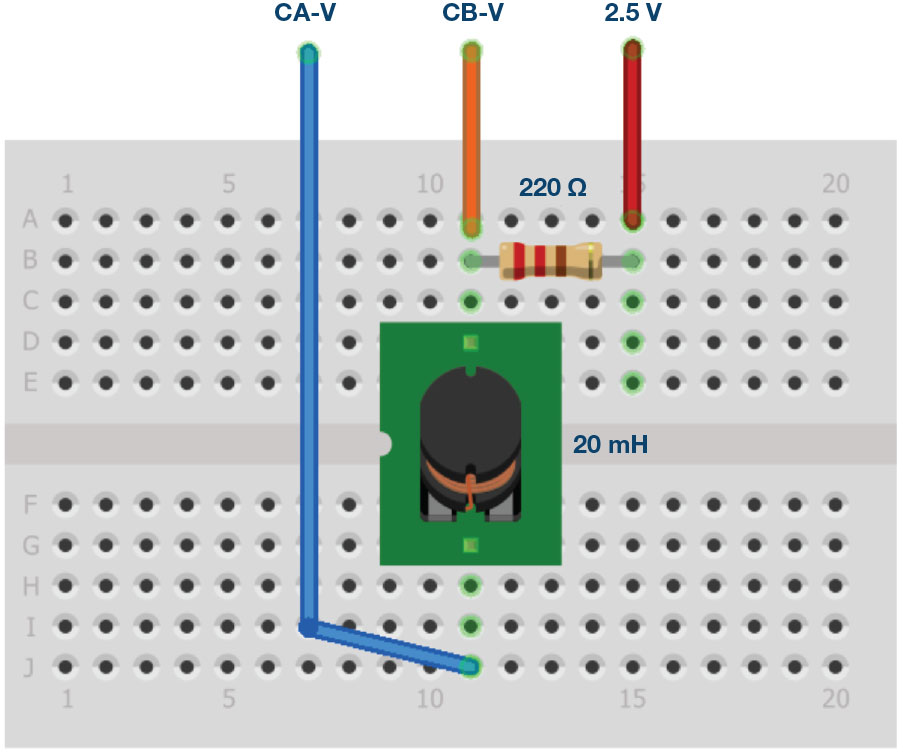
Set the Channel A AWG minimum value to 0.5 V and the maximum value to 4.5 V to apply a 4 V p-p square wave centered on 2.5 V as the input voltage to the circuit. From the AWG A mode drop-down menu, select the SVMI mode. From the AWG A shape drop-down menu, select Square. From the AWG B mode drop-down menu, select Hi-Z mode.

Calculate the applied frequency using Equation 2 for $t_{p} = 5 τ$

From the ALICE curves drop-down menu, select CA-V, CA-I, and CB-V for display. From the Trigger drop-down menu, select CA-V and Auto Level. Adjust the time base until you have at approximately two cycles of the square wave on the display grid.

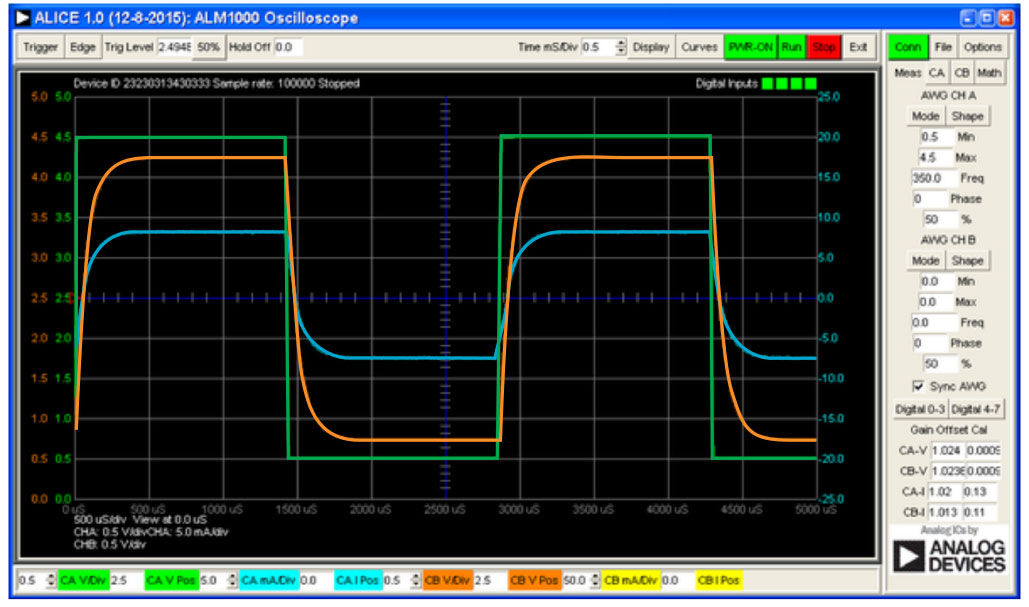
This configuration allows the oscilloscope to look at the input voltage of the circuit and the current through the inductor on Channel A and the output voltage of the circuit on Channel B. Make sure you have checked the Sync AWG selector.

The VR waveform has the same shape as the $I L (t)$ waveform. From the VR waveform, measure time constant t and compare that with the one that you calculated from $\frac{L}{R_{t o t a l}}$ (hint: find the time that corresponds to the 0.63 VR value). See the Background section for details.
Observe the response of the circuit and record the results again for $t_{p} = 25 τ$ and $t_{p} = 0.5 τ$ .

Questions:

Include the plots of IL and VR for different $t_{p}$ values, as given in Procedure 4.

A capacitor stores What do you think an inductor stores? You can find the answers at the StudentZone blog.

Notes

As in all the ALM labs, we use the following terminology when referring to the connections to the ALM1000 connector and configuring the hardware. The green shaded rectangles indicate connections to the ADALM1000 analog I/O connector. The analog I/O channel pins are referred to as CA and CB. When configured to force voltage/measure current, –V is added, as in CA-V or when configured to force current/measure voltage, –I is added, as in CA-I. When a channel is configured in the high impedance mode to only measure voltage, –H is added, as in CA-H.

Scope traces are similarly referred to by channel and voltage/current, such as CA-V and CB-V for the voltage waveforms, and CA-I and CB-I for the current waveforms.

We are using the ALICE Rev 1.1 software for those examples here. File: alice-desktop-1.1-setup.zip. Please download here.

The ALICE desktop software provides the following functions:

A 2-channel oscilloscope for the time domain display and analysis of voltage and current
The 2-channel arbitrary waveform generator (AWG) controls.
The X and Y display for plotting captured voltage and current voltage and current data, as well as voltage waveform histograms.
The 2-channel spectrum analyzer for frequency domain display and analysis of voltage
The Bode plotter and network analyzer with built-in sweep generator.
An impedance analyzer for analyzing complex RLC networks and as an RLC meter and vector
A dc ohmmeter measures unknown resistance with respect to known external resistor or known internal 50 Ω.
Board self-calibration using the AD584 precision 2.5 V reference from the ADALP2000 analog parts kit.
ALICE M1K voltmeter.
ALICE M1K meter source.
ALICE M1K desktop tool.

For more information, please look here.

Note: You need to have the ADALM1000 connected to your PC to use the software.

Doug Mercer [doug.mercer@analog.com] received his B.S.E.E. degree from Rensselaer Polytechnic Institute (RPI) in 1977. Since joining Analog Devices in 1977, he has contributed directly or indirectly to more than 30 data converter products, and he holds 13 patents. He was appointed to the position of ADI Fellow in 1995. In 2009, he transitioned from full-time work and has continued consulting at ADI as a Fellow Emeritus contributing to the Active Learning Program. In 2016 he was named Engineer in Residence within the ECSE department at RPI.

Antoniu Miclaus [antoniu.miclaus@analog.com] is a system applications engineer at Analog Devices, where he works on ADI academic programs, as well as embedded software for Circuits from the Lab® and QA process management. He started working at Analog Devices in February 2017 in Cluj-Napoca, Romania.

He is currently an M.Sc. student in the software engineering master’s program at Babes-Bolyai University and he has a B.Eng. in electronics and telecommunications from Technical University of Cluj-Napoca.