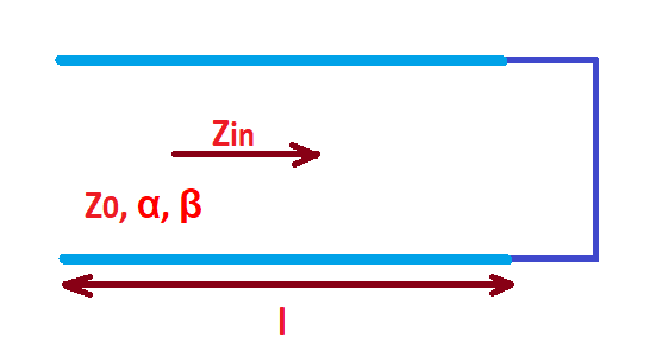
This post tells about short-circuited half wavelength line resonator. Half wavelength line resonator is depicted below, it is short circuited at one end.
This transmission line as characterised with characteristic impedance , propagation constant , attenuation constant , length , and resonant frequency .
Input impedance here .
In practice it is usually used low-losses transmission lines where , then . Let’s consider the transmission line in the conditions close to resonant , here is small.
Then , is a velocity of the transmission line. As we have half wavelength line resonator .
For the condition of resonance we have , , and . Input impedance can be presented as . So this transmission line can be presented as series RLC circuit, where , , and .
Resonance in short-circuited transmission line also happens for when .
Unloaded quality factor for this transmission line is .
More education information is available at our Reddit community r/ElectronicsEasy.