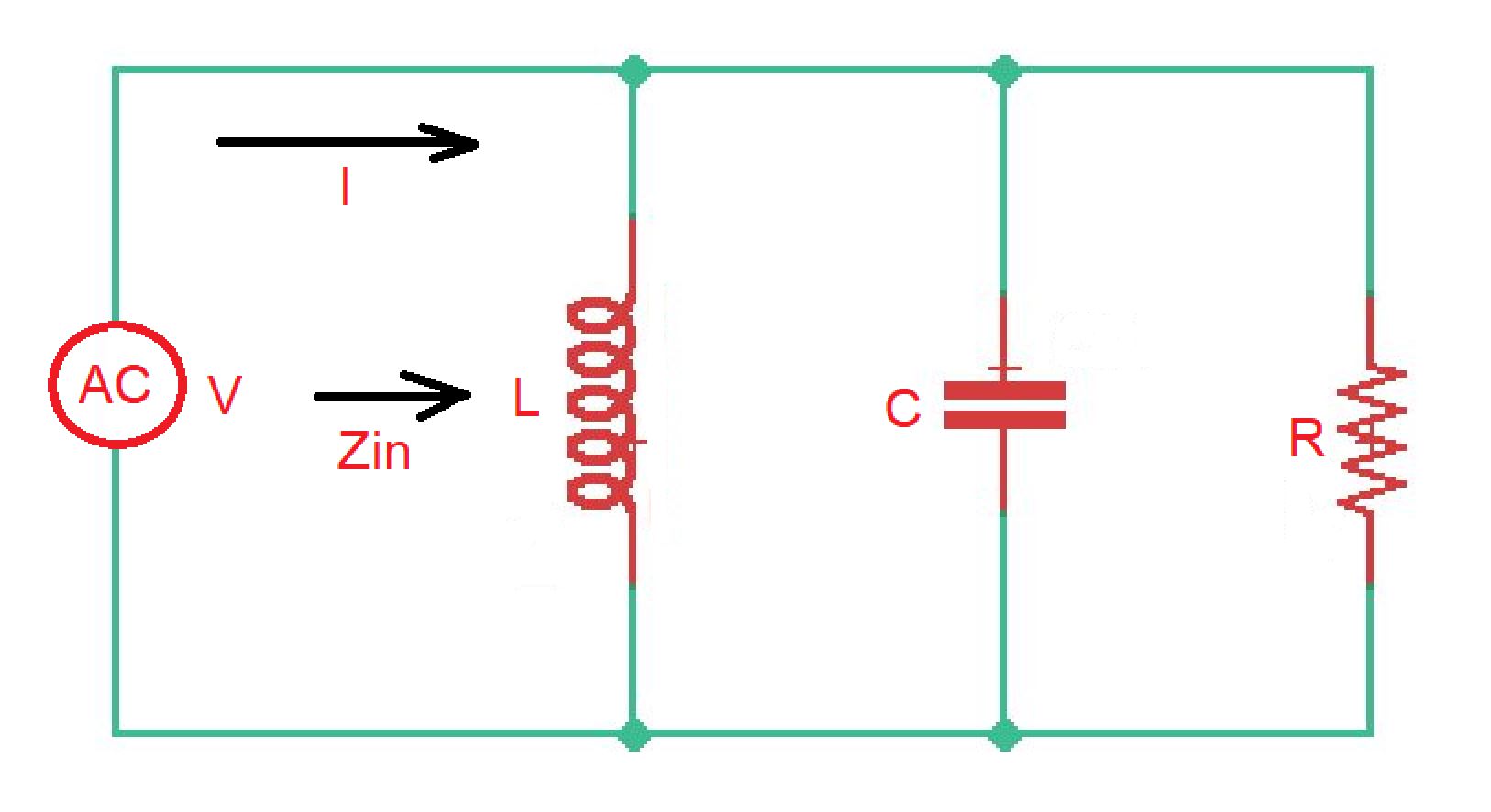
Parallel RLC resonant circuit is also used to model a resonator in the resonance mode. Resonator is a system, that is experiencing the resonance phenomena. Resonance in RLC circuit occurs when power stored at inductor is equal to power stored at capacitor.
The example of parallel RLC resonant circuit is depicted below.
In case of parallel connection . So power delivered to resonator is .
Power stored at the inductor is . Power stored at the capacitor is . And power that dissipates at the resistor .
So . Here we can find that .
Resonance phenomena occurs when energy stored at inductor is equal to energy stored at capacitor, then .
The resonance frequency here is (the same as for series RLC resonant circuit). Quality factor for unloaded RLC circuit is .
Let’s consider circuit behaviour near resonance frequency , where . So .