The matching impedance process for RF circuits is very important. Impedance matching is also called the tuning process. Physically it represents the circuit between the load and transmission line that can perform the following functions: it maximises the delivered power when the load is matched with the transmission line and minimises power loss; it improves the signal-to-noise ratio of the system; it also minimises the amplitude and phase errors. When considering the matching process it is important to keep in mind the following factors: complexity, bandwidth, adjustability and implementation aspects.
The simplest way of approaching the matching process is by using lumped components. Depending on the position of the normalised impedance on the Smith Chart, it can be used in one of two matching circuits: if the normalised impedance is inside the circle on the Smith Chart (Figure 1), then we must use the matching scheme depicted in Figure 2a, and if the normalised impedance is outside the circle of the Smith Chart, then the scheme in Figure 2b must be used.
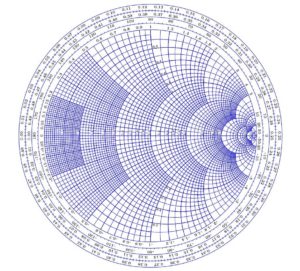
Figure 1. The Smith Chart (used in impedance matching).
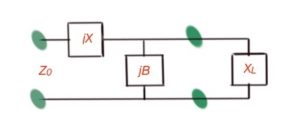
a
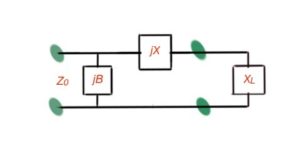
b
Figure 2. L-section impedance matching circuits.
Let’s consider the load resistance as .
If the normalised impedance is out of the circle, then , then and .
If the normalised impedance is in the circle , then , then , and .
In practice it is always easier to calculate the matching impedance using the Smith Chart.[1]
[1] “Microwave engineering”, 4th edition, David M. Pozar.