Linear electric circuits and linear circuit elements are those where resistance, capacitance and inductance are not dependent on the current or voltage magnitude and direction. Voltage and current are determined by linear algebraic or differential equations.
For example, if is not dependent on current or voltage , then Ohm’s Law is a linear function. The same applies if capacitance and inductance are not dependent on current or voltage , they are determined by linear differential equations. Concerning the linear and voltage sources, current source is linear when current is not dependent on the voltage drop on the current source; voltage source is linear when its emf is not dependent on current flowing through the source.
Unfortunately, real semiconductor components are not linear devices. As current flows through the conductor, it is heating up and its resistance changes. As the current changes in the inductor with the ferromagnetic core, its inductance changes. Depending on the isolator, its isolation changes as the function of charge, which means that capacitor isolation changes with the current flow. If in the specific work range for electronic components, current and voltage keep their linearity, they are considered linear. Linear circuits are easier to calculate, so if linear laws are applicable to the circuit with some proper proximity, circuits are considered linear.
In most electronic engineering departments current and voltage in the circuit are called actuating signals, and current and voltage that appear in the circuit are output signals.
There are two principles at work in a linear circuit – principles of superimposing and proportionality of signals. The principle of superimposing signals says that if actuating signals generated in the circuit and correspond to the output signals and , then for actuating signal corresponds output signal . The principle of proportionality of signals says that for actuating signal corresponds to the output signal .
Electric network is a graphic image of an electric circuit. It shows how electric elements interconnect to each other. Electric elements can be passive and active. Geometric elements are nods, branches and loops. To understand the difference, and to solve analytical problems, it’s important to understand main concepts.
Branch is created by a single element or more connected in series. In this way branch represents a two-terminal element.
Node is a connecting point for three or more branches in the circuit. Nodes are indicated as dots on the network.
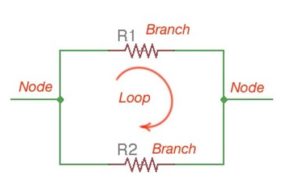
Any closed path in a network is called a loop. A loop starts at a node, passing through a set of nodes (only once) and finishing on the first node.
Two or more elements are in series if they belong to the same node and consequently carry the same current.
Two or more elements are in parallel if they connect by two or more nodes and carry the same voltage.
Voltage and current division - equivalent resistance for series connection