Equivalent voltage and current sources are equivalent – if you are replacing one with another and the rest of the circuit response is the same.
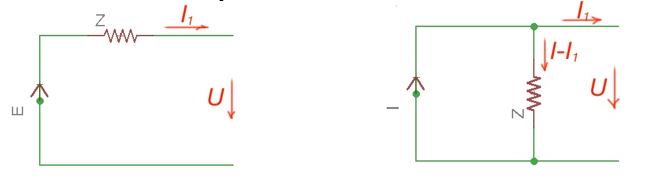
There are equivalent current and voltage sources shown in figure (in the nodal analysis post), producing , and the same current and voltage is applied to the rest of the circuit. Their equivalence condition is described by the formula , where is an internal complex resistance of both current and voltage sources.
The voltage on the voltage source terminals goes by the resistor voltage subtracted from EMF . And the voltage on the current source terminals is equal to the voltage on the resistor with the complex resistance as . In both cases . It means we are getting the condition of source equivalence.
However, the power of both current and voltage sources are different. Voltage source power is equal to , power consumed on the current source is . It means the equivalence of current and voltage sources has to be used only in terms of unchangeable currents, voltages and powers.