Let us talk about the importance of replacing real circuit components by their ideal circuit elements, taking into account complex factors. Representation of resistance, inductance and capacitance as ideal elements of an electric circuit is based on the assumption that energy losses, magnetic and electric fields are concentrated in separated and different parts of the electric circuit. Separated via consideration of resistance, inductance and capacitance is an approximate method. In reality energy losses, electric and magnetic fields are interconnecting with each other.
Electrical conductivity of any isotropic substance is characterised with conductivity, which is equal to the ratio of current density and electric field. The parameter inverse to conductance is resistance. Resistance of a conductor in the condition of constant current is equal to the ratio of a conductor’s voltage to its DC current. From another side resistance depends on the length of the conductor , cross-section area and its resistivity : .
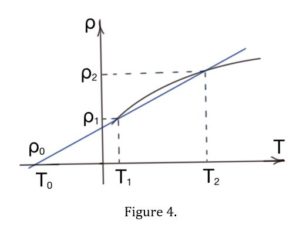
In the wide range of temperature dependence of the conductor resistivity, resistivity on temperature is rectilinear. For metals p = f(T) is increasing, for isolators and electrolytes it is decreasing.
Let us assume and resistivity with the temperatures and , and is the crossing point of the with axis, then we have the following proportion: .
The concept of resistance is related to energy losses, i.e. irreversable process of energy absorption. The amount of heat released when current passes through a semiconductor depends on a range of factors, including current frequency. When current frequency is small, resistance is equal to the resistance with direct current (DC). When current frequency is increasing, current distribution across the conductor section is uneven. Current density is decreasing inside the conductor, and current is displaced to its surface – this effect increases resistance and is called surface effect.
Uneven current distribution across the conductor section and heat losses increasing can also be caused by the current of the nearby conductor. This is called proximity effect.
Alternating magnetic field creates eddy currents in condutive environments, which causes additional heat losses. Moreover, magnetic field radiation also increases conductor resistance and energy losses. Electric and magnetic fields create some inductance and capacity in the conductor. Calculating resistance, conductance and capacitance with the factors described above also involves field theory.
Let us take a simple inductor with current flowing through it. The DC current inductance voltage on its terminals is determined by the voltage drop on the inductance resistance – current is the same for all its coils.
In case of AC current, the situation will be more complex. Alternating magnetic field creates electro-magnetic force (EMF) of self-inductance on the inductor coils. The electric field for every coil of inductor will be alternating. Current on each coil becomes different. It leads to the bias current between coils. The higher AC current frequency, the higher emf of self-inductance and bias current. With low AC current frequency we can neglect bias current; with high AC current frequency we can not neglect bias current, it can be commensurate with AC current, and even higher. It means, depending on AC current frequency, inductance can be represented as a resistance ; or inductance with series resistance ; or inductance and series resistance , with parallel capacitance .
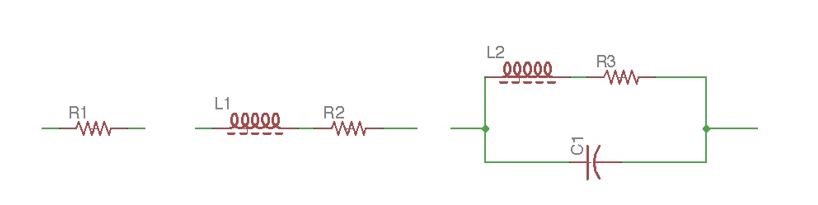
If an inductor has many coils, AC current, flowing through it creates magnetic flow, proportional to the coils number. Considering that magnetic flow is connected to all coils, it can be assumed that self-inductance flow and inductance are proportional to the square of the number of the inductor coils.
Let us take an inductance with coils, mounted on a long core with length , and cross-section , Let us take as the permeability of the core. Magnetic flow in the core is determined by the rate of magnetising force of the inductor to the core reluctance: :
Then according to the definition of inductance .
it determines by the size of the inductor, permeability of it’s core and square of number of its coils.
Let us consider a capacitor with two conductors and isolator between them.
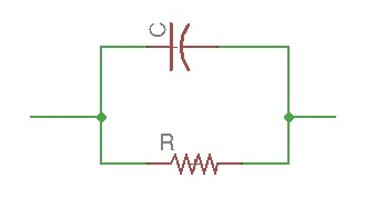
When the voltage is constant and the isolator is ideal, current in the circuit is absent. If voltage is alternating, changes of charge in a system stimulates alternating current, which creates alternating magnetic field. Effects, created by magnetic field, can be taken into account putting an inductance into the electrical circuit scheme series with the capacitor. Usually this inductance is neglected, because it’s small. A real isolator has some conductance that leads to heat losses. These heat losses can be counted, adding a resistance r into the circuit scheme, in parallel with capacitance .
As we know, capacitance is determined by the size of the conductor plates , distance between them and isolator characteristics: .
If isolator thickness is small compared to capacitor size, capacitance can be calculated by the following formula: .
We must always take into account that the higher circuit frequency and the bigger component size, interconnection and inseparability of electric and magnetic fields in the circuit grows and becomes complex and uniform.