What is capacitor and how does it work

This post answers the question: “What is capacitor and how does it work?”. Here we consider the capacitance concept and it’s main feature. As soon as we are considering not only effective capacitors and inductors in the circuit, but also parasitic capacitances and inductances, it is important to consider how these effects work.

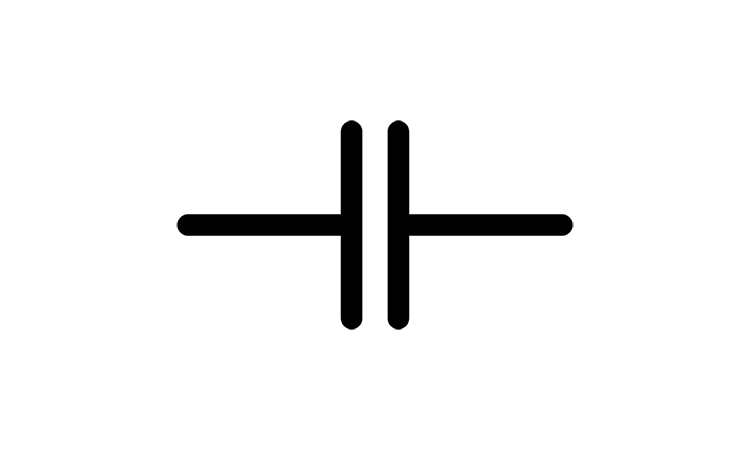
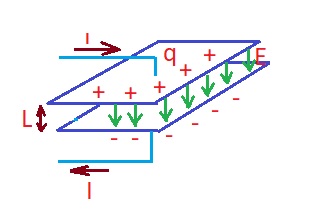
Linear capacitor is depicted on the figure below. Two capacitor plates are considered parallel with the $l$ gap between them, that is filled with linear insulator with permittivity $\epsilon$. if there is an electric current goes to the positive plate of capacitor, the charge $q$ is being transported on the positively charge plate. At the same time, the same current exist on the other plate of the capacitor, that transports charge from the plate.

The charge $q$ on the positive plate and negative charge $–q$ on the other plate create electric field within a dielectric $E\left(t\right)=\frac{q\left(t\right)}{\epsilon A\left(t\right)}$ with direction from one plate to another. This electric field creates $v\left(t\right)=l\left(t\right)E\left(t\right)$, so $E\left(t\right)=\frac{\epsilon A\left(t\right)}{l\left(t\right)}v\left(t\right)$. Then capacitance $C\left(t\right)=\frac{\epsilon A\left(t\right)}{l\left(t\right)}$ and charge can be found $q\left(t\right)=C\left(t\right)v\left(t\right)$.

Electric current, the charge rate transported to the positive plate of capacitor $i\left(t\right)=\frac{dq\left(t\right)}{dt}$. If we will use the equations above: $i\left(t\right)=C\frac{v\left(t\right)}{dt}$.

The main feature of a capacitor is a memory feature.

From the differential equation for charge we can get $v\left(t\right)=\frac{1}{C}{\int }_{–\infty }^{t}i\left(t\right)dt$, and as soon as $\frac{d{\omega }_E\left(t\right)}{dt}=i\left(t\right)v\left(t\right)$ then ${\omega }_E={\int }_0^{q}v\left(q\right)dq$. It means that ${\omega }_E\left(t\right)=\frac{q^2\left(t\right)}{2C}$ or ${\omega }_E\left(t\right)=\frac{C{v}^2\left(t\right)}{2}$ is a stored energy in a capacitor.

Educational content can also be reached via Reddit community r/ElectronicsEasy.