Step inputs with capacitors and inductors

This post tells about step inputs in the capacitive or inductive circuit. Here we consider four cases of step functions with capacitor and inductor.

Let’s first consider current source, driving the capacitor as depicted below.

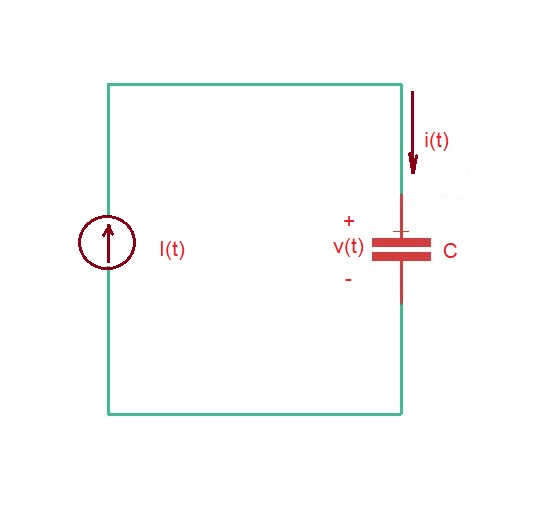
The step input of the current source is $I=\left\{\begin{array}{l}0, t<0\\ I_0, t\ge 0\end{array}\right.$ that gives us voltage $v\left(t\right)=\left\{\begin{array}{l}0, t<0\\ \frac{I_{0}t}{C}, t\ge 0\end{array}\right.$. The voltage and current forms are shown below.

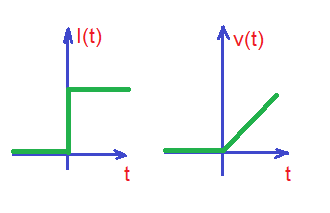
It clearly shows stored charge in the capacitor, and voltage here is a continuous function of time. However, as we can see the current here discontinuous function of time, and voltage and charge are continuous functions of time here.

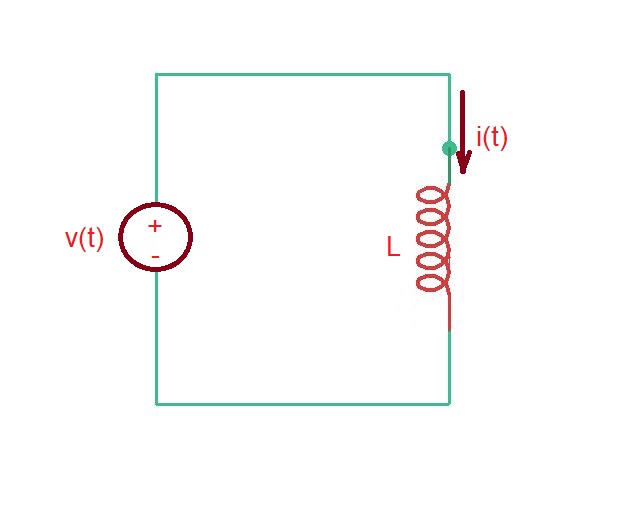
Let’s consider voltage source driving an inductor (on the figure below).

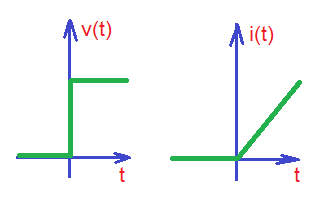
The voltage waveform is $V\left(t\right)=\left\{\begin{array}{l}0, t⩽0\\ V_0, t>0\end{array}\right.$(discontinuous function), current here will be time dependent and continuous function, $i\left(t\right)=\left\{\begin{array}{l}0, t\le 0\\ \frac{V_{0}t}{L}, t>0\end{array}\right.$  and so the flux linked to an inductor. Voltage and current functions are depicted on the figure below.

Let’s consider a circuit, where voltage source driving capacitor (below).

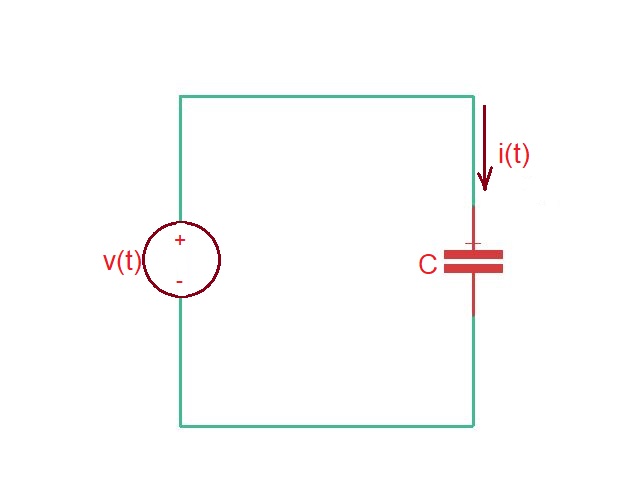
The voltage waveform is $V\left(t\right)=\left\{\begin{array}{l}0, t\le 0\\ V_0, t>0\end{array}\right.$. As soon as we are dealing with the discontinuous voltage step function, the waveform can be presented as , where  function is depicted below.

At the same time $u\left(t\right)={\int }_{–\infty }^t\delta \left(t\right)dt$ or $\delta \left(t\right)=\frac{du\left(t\right)}{dt}$ and ${\int }_{–\infty }^{\infty }\delta \left(t\right)dt=1$.

As the result we have the following equation for current $i\left(t\right)=C{V}_0\delta \left(1\right)$. Waveforms for voltage and current are depicted below.

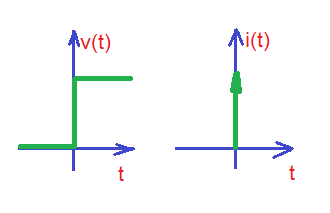
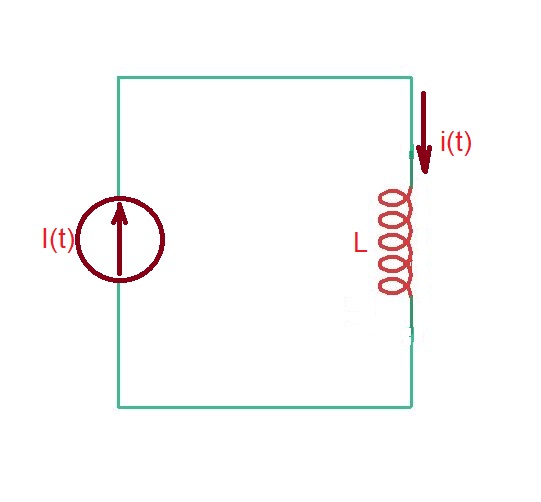
Now let’s consider current step source driving inductor (figure below).

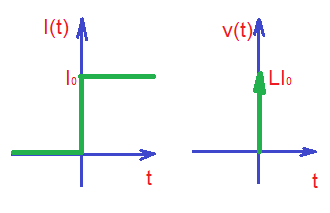
The waveform for current is $I\left(t\right)=\left\{\begin{array}{l}0, t\le 0\\ I_0, t>0\end{array}\right.$ and the voltage waveform is $v\left(t\right)=L{I}_0\delta (t, T)$ (depicted below).

Educational content can also be reached via Reddit community r/ElectronicsEasy.