Series RL circuit analysis

This post answers the question “What is a series RL circuit?”. It shows how to make an analysis of series $RL$ circuit with the step input signal.

The circuit and the input voltage signal are depicted below. Let’s find voltage and current wave-forms of the inductor and it’s time constant.

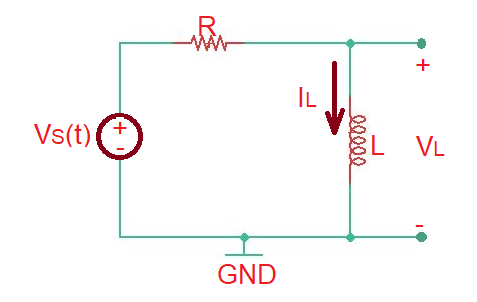
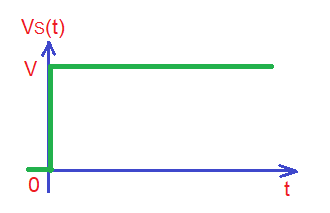
Let’s consider the voltage source signal as $V_S\left(t\right)=\left\{\begin{array}{l}0, t<0\\ V, t\ge 0\end{array}\right.$.

As in the example with the series RC circuit, we must apply KVL  $i_{L}R+L\frac{d{I}_L}{dt}=v_S$. The total solution of this differential equation is the sum of homogenous and particular solution.

In order to find homogenous solution we must resolve the equation $i_{L}R+L\frac{d{i}_L}{dt}=0$. Let’s assume that homogenous solution is in the form $i_L=A{e}^{st}$. So $RA{e}^{st}+sL{e}^{st}=0$, then $s=–\frac{R}{L}$ and the homogenous solution is $i_L=A{e}^{–\frac{R}{L}t}$.

In order to find particular solution, we must resolve the equation $v_S=i_{Lp}R+L\frac{d{i}_{Lp}}{dt}$. Particular solution of this equation can be $i_{Lp}=const$. In this case $const=\frac{V}{R}$.

So total solution is $i_L=\frac{V}{R}+A{e}^{–\frac{R}{L}t}$. Knowing that for $t=0$, $i_L=0$ then $A=–\frac{V}{R}$. Then $i_L=\frac{V}{R}(1–e^{–\frac{R}{L}})$.

Here we can obtain $v_L=L\frac{d{i}_L}{dt}=V{e}^{–\frac{R}{L}t}$.

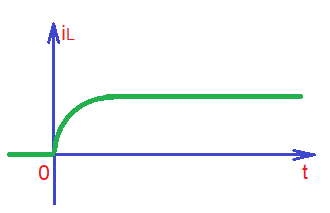
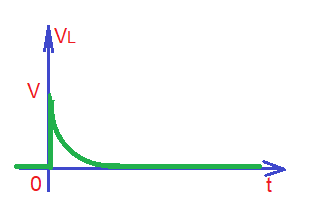
The current and voltage waveforms for inductor are depicted below.

Educational content can also be reached via Reddit community r/ElectronicsEasy.