Digital concept of a MOSFET
Electrical switch (MOSFET) is a three terminal device that can perform two states – ON and OFF. In the ON state the electrical switch is conducting, in the OFF state the electrical circuit is open.
The switch has an output, gate and input terminals. The gate terminal is named G, and the output and input terminals are symmetric. The gate terminal is the controlling terminal. The input terminal is labelled S as a source, the output terminal is labelled D as a drain. Figure 1 shows the current and voltages in the MOSFET. The gate current is , the drain-to-source current is , the gate-to-source voltage is , and the drain-to-source voltage is .
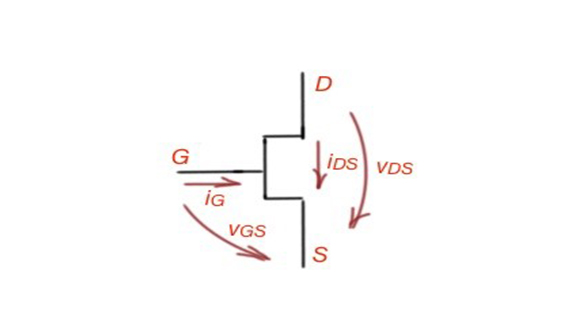
Figure 1. Currents and voltage scheme in a MOSFET.
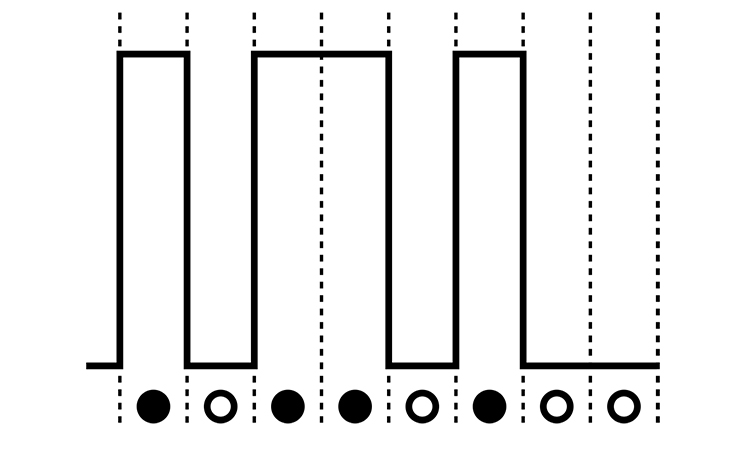
When the gate terminal has the logic ‘1’, the MOSFET is instructed to conduct – to be in ON state. Otherwise the switch is instructed to be OFF and the circuit is open, and it does not conduct. Figure 2 shows the MOSFET states. The logical functions can also be performed using switches, for example, the OR logic function can be made by two MOSFET in parallel, and the AND function can be performed using MOSFETs in series.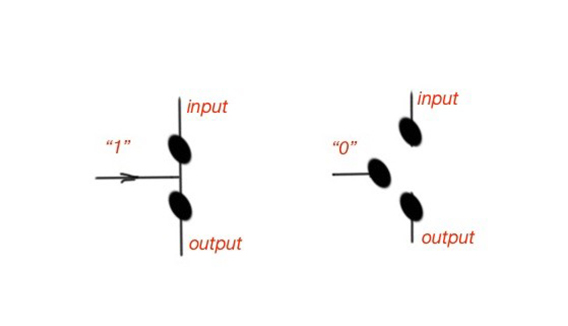
Figure 2. Logical interpretation of a MOSFET.
A MOSFET is characterised by the S model, or Switch model. The MOSFET is in an ON state when the is bigger than , when it is less, the MOSFET is OFF. The S model describes the connection between S and D terminals of the MOSFET when the device is in an ON state. The resistance between S and D terminals is expected to be ignored. In the OFF state there is an open circuit between the drain and source. To be technically correct the MOSFET operation is controlled by the gate-to-source voltage . The S model for the MOSFET can be shown by the following: when , , when ,.
Figure 3 shows the S model characteristics for a MOSFET. [1],[2]
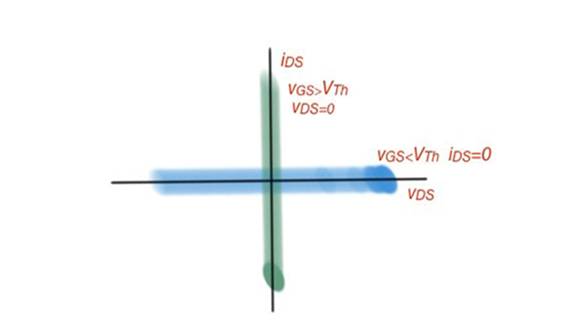
Figure 3. V-I curve for a MOSFET in ON and OFF state.
[1] «Foundations of analog and digital circuits», A. Agarwal, Elsevier.
[2] «MOSFET handout», www.berkeley.edu.
MOS transistor digital representation
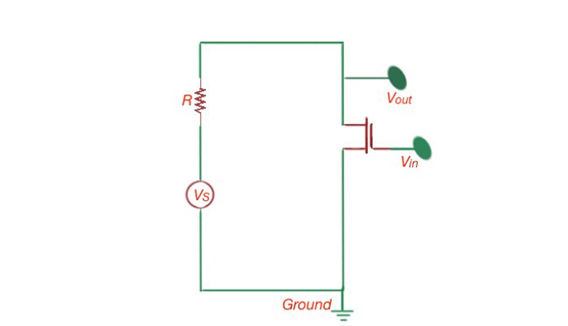
Figure 4 represents the MOSFET transistor function. Let’s consider the Gate-Source as input and Drain-Source as output. Here the Gate is connected to the input, the Source is connected to R, and the Drain is connected to E.
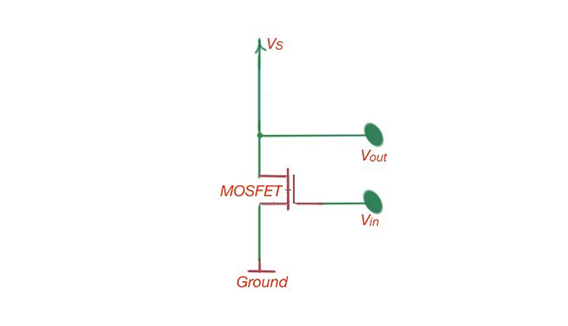
The MOSFET is the important building block for the construction of different devices. Figure 5 shows the inverter model, which can also build s-models, and transfer input-output characteristic as we did in previous modules.
Figure 6 represents n-input NAND models and Figure 7 represents its S model. MOSFETs can be applied to represent different logic expressions, for example , that are shown in Figure 8.
a
 b
b
Figure 4. The MOSFET circuit (a), and its s-model representation (b).
Figure 5. A MOSFET model drawing.
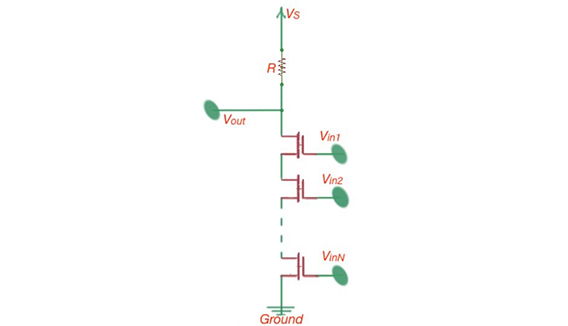 Figure 6. N-channel NAND gate circuit.
Figure 6. N-channel NAND gate circuit.
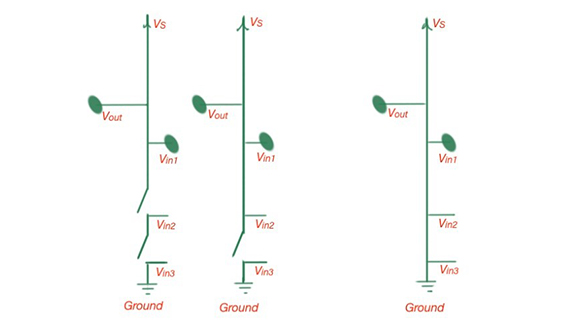
Figure 7. The s-model of an n-channel NAND gate.
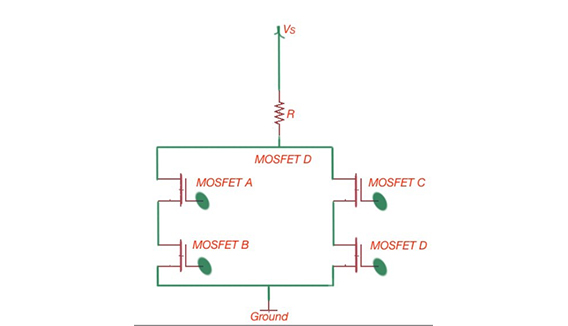
Figure 8.The transistor-level representation of .
MOSFETs are very good for creating gates, because their output does not affect the input. When building a device containing multiple gates, it’s important to know that surrounding MOSFETs are not affecting the logical functions of the gate.
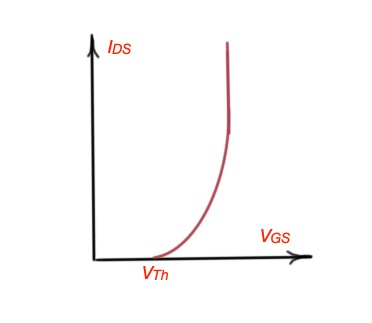
As was explained at the beginning, the logical function of the gate is based on the threshold levels (Figure 2 of Digital Systems and Design Part 1). The input-output characteristics of the designed logic device can easily show if it corresponds to the input and output threshold levels. The example is depicted in Figure 9.
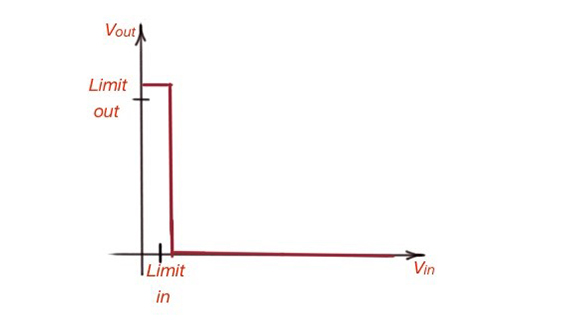 Figure 9. The input-output characteristics for a MOSFET.
Figure 9. The input-output characteristics for a MOSFET.
The classical S-model of a MOSFET does not take into account the resistance between D and S of the MOSFET. So in the model assume the resistance between D and S is called the SR model, or switch-resistor model. When the switch is off, there is no current between S and D.
When the gate voltage is bigger than the threshold voltage, the switch is ON , current flows between D and S, and we must take into account the resistance between D and S. The MOSFET work regime when ≪– is characterised with resistance that is not fixed but varies with , and when is greater then , the D-S region is not resistive.
However, the SR model is satisfactory for designing the logic devices. The SR model of the MOSFET can be presented in the following way: .[1] [1] «Foundations of analog and digital circuits», A. Agarwal, Elsevier.
The MOSFET structure, gain and power
MOSFETs are fabricated with a few steps of the CMOS manufacturing processes on the planar silicon wafer. These processes include n-well, p-well or both fabrications. The MOSFET fabrication technology has developed significantly since the 1960s, but as standard consists of the following steps:
- Substrate preparation;
- Oxidation process;
- Photoresist application;
- Mask application;
- Photoresist removing;
- Etching;
- N-well layer formation;
- layer removing;
- Polysilicon layer deposition;
- Gates creation;
- Oxidation;
- Masking;
- N-diffusion;
- P-diffusion;
- Oxide layer application;
- Metallisation;
- Terminals creation and assigning.
The structure of the MOSFET and it’s microscope photo is depicted in Figure 10.
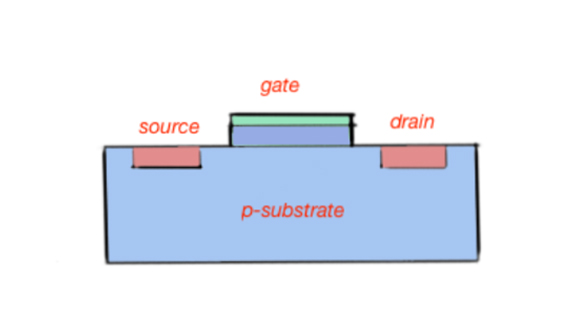
a
 b
b
Figure 10. (a) schematic structure of a MOSFET; (b) the FET microscope picture (property of Toshiba)[1]
As we know, as the channel between drain and sources forms, so the MOSFET goes to the ON state , and the current starts to flow when . The conducting channel between drain and source will be characterised with the resistance , here L,W are geometry characteristics of the channel and is the resistance of the channel per piece of square.
Let’s consider the SR model of the MOSFET. When the , then the MOSFET is in the ON state, and it experiences the resistance and the output voltage of the MOSFET is . This equation is very helpful when we design different MOSFET combination structures, so the condition of the next MOSFET to be turned on should be >.
For example, if we have the NAND gate, the output voltage for this MOSFET combination should be . If the MOSFET is used with the amplification feature, taking into account the noise margins of the device, the gain can be found using the formula (Figure 2 of voltage levels in digital systems). [2]
[1] “Toshiba wants to reshape the chip industry with new low-power tunnel FETs, $2 billion investment.”, www.extremetech.com.
[2] “Foundations of Analog and digital electronic circuits”, Anant Agarwal and Jeffrey J. Lang, Elsewier.
MOSFET characteristics
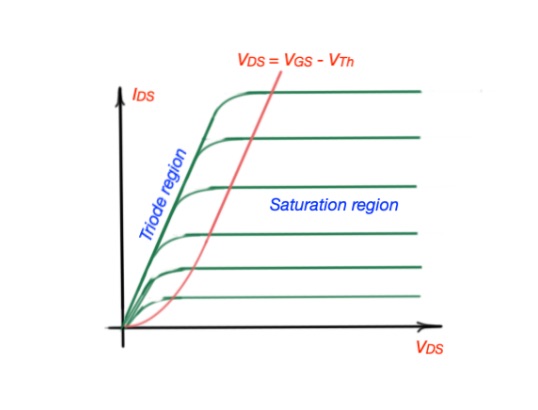
As we know MOSFET can be characterised in three regions – triode, saturation, cut-off.
Cut-off region : .
Triode region : .
Saturation region: .
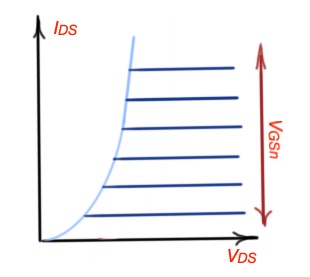
is a boundary between triode region and saturation region of the MOSFET, that can be described as linear functions separately.Horizontal parts can be represented as the current source. Horizontal lines are depend on the values of voltage. This model is called switch controlled source (SCS).
Triode region can be approximated as a straight line with a slope . So for a fixed and we have a linear function of and .MOSFET operation in this region can be approximated by SR model.
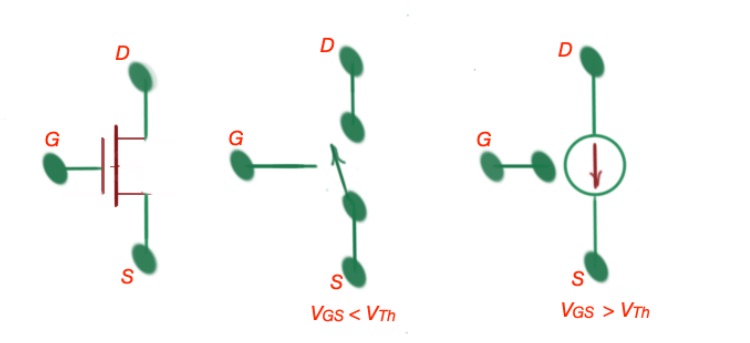
Switch-current source model (SCS).
Condition for applying this model is . The MOSFET states are depicted on the figure below.
When MOSFET is OFF. When and current from the source to drain is .
Graphically relations and are depicted on figures below.
So we can describe the saturation region of MOSFET operation as : .
(“Foundations of analogue and digital electronic circuits”, Anant Agarwall and Jefferey H. Lang, Elsevier).