Different types of controlled sources

This post answers the question “What are different types of controlled sources?”. Controlled sources are sources, that are dependent on some parameters of the system.

There is four types of controlled sources: voltage-controlled current source, current-controlled current source, current-controlled voltage source, voltage-controlled voltage source.

Controlled or dependent sources are mostly used for modelling behaviour of the devices with multiple terminals, like transistors or amplifiers. Very often for simplicity, modelling of devices occurs with linear dependent sources.

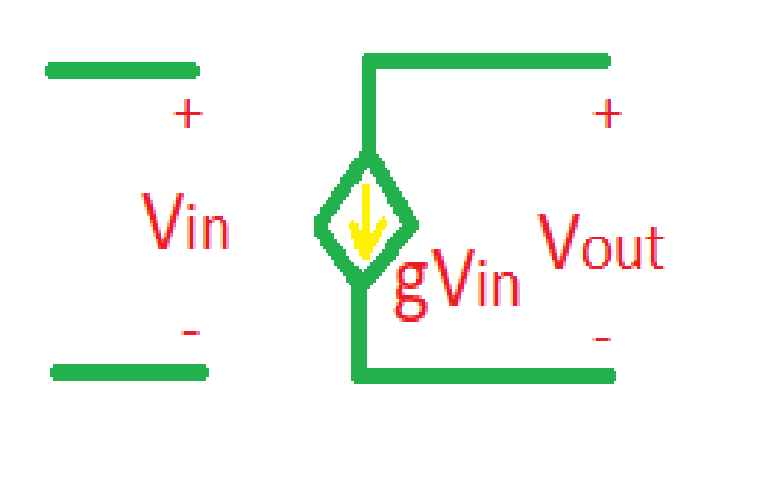
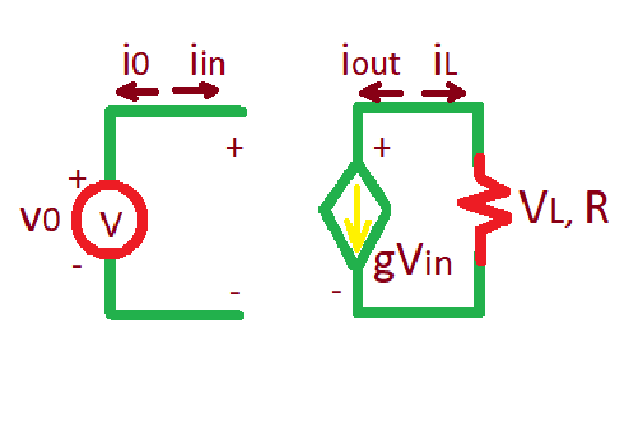
A circuit for linear voltage-controlled current source (VCCS) is depicted below. VCCS is described with the following equation $i_{out}=g{v}_{in}$, where $v_{in}$ is an input voltage and $i_{out}$ is an output current. Coefficient $g$ here is called transconductance.

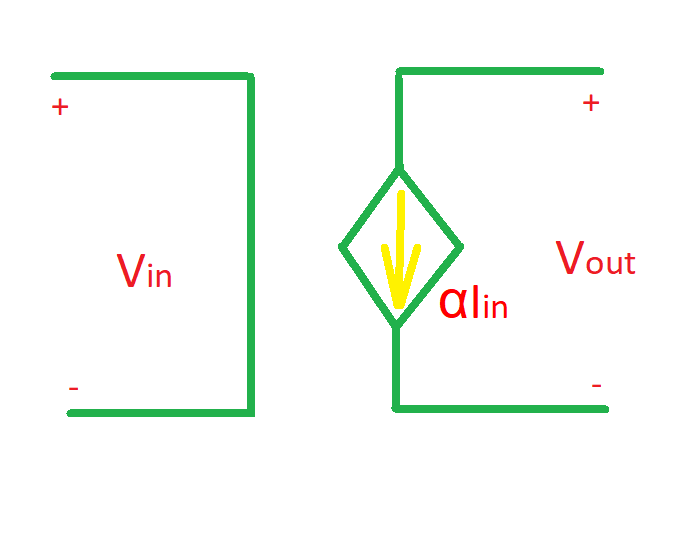
A circuit for linear current-controlled current source (CCCS) is depicted below. CCCS is described with the following equation $i_{out}=\alpha i_{in}$, where $i_{in}$ is an input current and $i_{out}$ is an output current. Coefficient $\alpha$ here is called current transfer ratio.

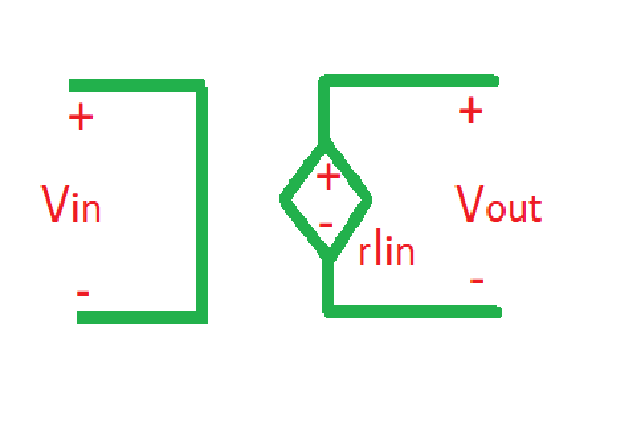
A circuit for linear current-controlled voltage source is depicted below. CCVS is described by following formula $v_{out}=r{i}_{in}$, where $i_{in}$ is an input current and $v_{out}$ is output voltage. Coefficient $r$ here is called transresistance.

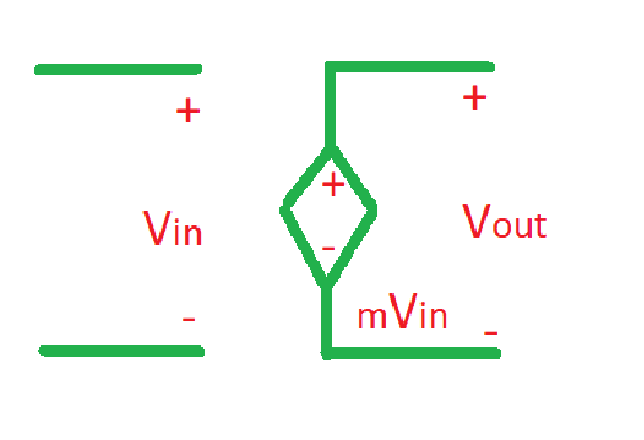
A circuit for linear voltage-controlled voltage source is depicted below. VCVS is described by following formula  $v_{out}=\mu v_{in}$, where $v_{in}$ is an input voltage and $v_{out}$ is an output voltage. Coefficient $\mu$ here is called voltage transfer ratio.

As seen above, if the controlling variable is voltage, the control part of the circuit is an open circuit. If the controlling variable is current, then the control part is short circuit.

How to solve the circuits with dependent sources? You must apply the following steps:

• Write all initial data and known variables
• Write Kirchhoff’s Current Laws
• Write Kirchhoff’s Voltage Law
• Solve the equations.

For example, for voltage-controlled voltage source with load (depicted below), we have the following equations.

Initial data:

$$\begin{gathered} v_0=V \\ {i}_{in}=0 \\ {v}_L=R{i}_L \\ {i}_{out}=g{v}_{in} \end{gathered}$$

Kirchhoff’s Current Laws:

$$\begin{gathered} i_0=–i_{in} \\ {i}_L=–i_{out} \end{gathered}$$

Kirchhoff’s Voltage Laws are:

$$\begin{gathered} v_0=v_{in} \\ {v}_L=v_{out} \end{gathered}$$

Resolving these equations we have:

$$\begin{gathered} i_0=i_{in}=0 \\ {v}_0=v_{in}=V \\ {i}_{out}=–i_L=–gV \\ {v}_{out}=v_L=–gRV \\ {p}_{in}=v_{in}{i}_{in}=0 \\ {p}_{out}=v_{out}{i}_{out}=g^{2}R{V}^2 \end{gathered}$$

More educational and technical posts you can read at our Reddit community r/ElectronicsEasy.

Reference: “Foundations of analog and digtal electronic circuits”, Anant Agarwal, Jeffrey H. Lang