Energy and charge conservationmin the circuit

This post tells about energy and charge conservation in the circuit. We will consider conservation laws on the circuit with two capacitors in parallel via the switch.

Let’s consider the circuit depicted below.

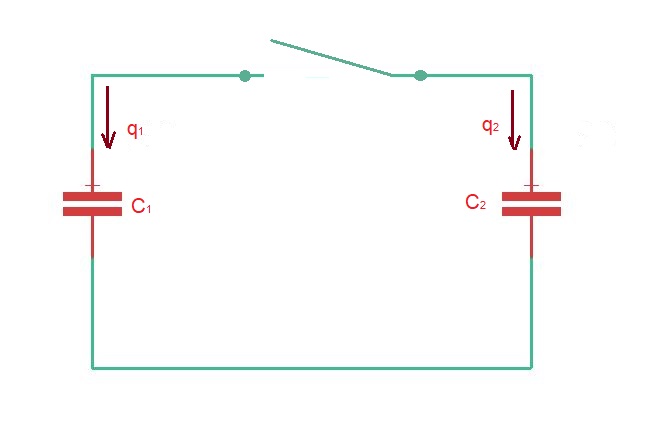
Circuit with two capacitors connected in parallel via the switch

Here in accordance to the Kirhhoff Current Law we have $\frac{d q_{1} (t)}{d t} + \frac{d q_{2} (t)}{d t} = \frac{d (q_{1} + q_{2})}{d t} = 0$ . At the same time $v_{1} = v_{2}$ here and $\frac{q_{1} (t)}{C_{1}} = \frac{q_{2} (t)}{C_{2}}$ . At the same time we know that $q_{1} (t) + q_{2} (t) = C_{1} + C_{2}$ .

Then $q_{1} (t) = \frac{C_{1}}{C_{1} + C_{2}} (Q_{1} + Q_{2})$ and $q_{2} (t) = \frac{C_{2}}{C_{1} + C_{2}} (Q_{1} + Q_{2})$ .

From here we have $v_{1} = v_{2} = \frac{Q_{1} + Q_{2}}{C_{1} + C_{2}}$ .

After the moment of switch closure, charge in the circuit is conserved.

Let’s see what happens with energy in the circuit before and after switch closure. Before switch closure the total energy in the circuit $w_{E} = \frac{{Q^{2}}_{1}}{2 C_{1}} + \frac{{Q_{2}}^{2}}{2 C_{2}}$ . After the switch is closed $w_{E 1} = \frac{{q_{1}}^{2} (t)}{2 C_{1}} + \frac{{q_{2}}^{2} (t)}{2 C_{2}}$ . It means that energy in the circuit after switch is closed is not conserving. More over, it is easy to see that $w_{E} - w_{E 1} > 0$ .

Educational content can also be reached via Reddit community r/ElectronicsEasy.