Boolean logic. Truth tables for logic expressions.

Digital circuits implement logic using “if-statements”. The simplest logic operations are $AND, OR, NOT$.

$AND$operation is represented with “*”, $OR$ operation – with symbol “+”, $NOT$ operation – with operation “$\overline{}$”

Example $AND$ statement: $Z=X AND Y$, that means if $X$ is true $AND$ $Y$ is true, then $Z$ is true, otherwise $Z$ is false. Statement is true, when both elements $X$ and $Y$ are true.

Example $OR$: $Z=X OR Y$, if $X$ is true or $Y$ is true, then $Z$ is true, otherwise $Z$ is false. Statement is true, when one of the  elements $X$ or $Y$ is true.

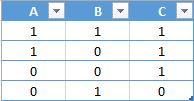
Every logic expression can be described with the truth table. Truth table numerates every possible input value and every possible output value using Boolean functions. Every TRUE correspond to logic  “1”, every FALSE correspond to logic “0”. So if we will consider the logical statement $C=A+\overline{B}$, that means $C$ is true (“1”), if $A$ is true (“1”) $OR$ $B$ is false (“0”), otherwise $C$ is false (“0”). Truth table for this statement shows every possibility of this statement in its logical representation, i.e.

Let’s see what happening at the truth table above:

1 line: $A$is true (“1”), $B$is true (“1”), then $C$ is true (“1”).

2 line: $A$ is true (“1”), $B$ is false (“0”), then $C$ is true (“1”).

3 line: $A$ is false (“0”), $B$ is false (“0”), then $C$ is true (“1”).

4 line: $A$ is false (“0”), $B$ is true (“1”), then $C$ is false (“0”).

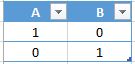
Truth table for the statement $B=\overline{A}$, that means $B$ is true (“1”), if $A$ is false (“0”), else $B$ is false (“0”).

1 line: $A$ is true (“1”), then $B$ is false (“0”).

2 line: $A$ is false (“0”), then $B$ is true (“1”).

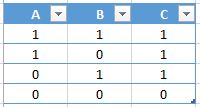
Truth table for $A+B=C$. Here if $A$ is true (“1”) or $B$ is true (“1”), then $C$ is true (“1”), else $C$ is false (“0”).

1 line: $A$ is true (“1”), $B$ is true (“1”), then $C$ is true (“1”).

2 line: $A$ is true (“1”), $B$ is false (“0”), then $C$ is true (“1”).

3 line: $A$ is false (“0”), $B$ is true (“1”), then $C$ is true (“1”).

4 line: $A$ is false (“0”), $B$ is false (“0”), then $C$ is false (“0”).

Truth table can contain any amount of input values, it will create bigger amount of output values. Bigger amount of input values – bigger amount of output values.