In this chapter we will cover magnetic interaction. Magnetic interaction shows how charged particles are interacting with each other. A charge moving in a current experiences the perpendicular force that arises with a charge velocity. The value of this force is proportional to the charge q and it’s velocity v.
This force has two parts – electric and magnetical: F = qE+q[v,B]. Vector B is magnetic induction, and this is a characteristic of a magnetic field.
Describing the magnetic field and induction is useful when using the term turn of current. This turn of current is suppose to be a frame of small size with a current through it. The magnet momentum of this frame is P = ISn, where I is a current through frame, S is a square of a frame, and n is a normal vector to the frame plane. In the magnet field this frame is affected by the moment of rotating force. Magnetic induction vector B is characterised by magnetic force on currents or moving charges. Magnetic induction has several features:
- B direction correlates to the direction magnet momentum Pm, A * m2
- B measurement units are Ts, Tesla
- Taking into account that magnetic force momentum N = [p,B], module of vector B can be defined as a ratio of modules of magnetic force momentum and magnetic momentum
Magnetic field is characterised by the principle of superposition, that states: if in point A of space, currents and charges create magnetic fields with inductions B1, B2… Bn, then the summarised magnetic field for point A is B=B1+ B2 … + Bn.
French scientists Biot and Savart have conducted several expriments, monitoring magnetic field induction for different conductors. Scientist Laplace has analysed this experimental data and made an approximation for magnetic induction B that is a sum of the elements dB for elementary pieces of current in every point of space – sum opeartion here can be replaced with integral
– Figure 27. This formula is called the Law of Biot-Savart-Laplace. The constant
is called vacuum permeability. Vector B direction is perpendicular to the fragment of current dr, and vector r. For Figure 27, B is directed into the screen. The module of magnetic induction vector
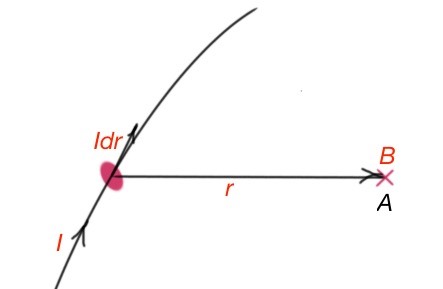
For example, let’s calculate the induction of magnetic field for a long wire in the magnetic field.
To determine the structure of a magnetic field in any part of space, magnetic induction lines are used. Magnetic induction lines are the lines tangent to those that correlate with the vector of magnet induction B. Similar to the electric field, the strength of magnetic field is proportional to the magnetic field lines density. For uniform magnetic field, magnetic field lines are parallel lines, equally distanced from each other.
Induction magnetic field lines are always enclosed. The equation depicting the behaviour of magnetic induction is ∫ BdS = 0. Magnetic induction lines never counter-cross.
Let’s determine the magnetic field for a charged particle. A charged particle can be considered as a fragment of current, characterised by the dr vector I = jS where
and