Electric charge is a measure of the elementary particles that enable electrical and magnetic interactions. Electric charge, is the basis for Coulomb Law, and has some fundamental features, which can be described as:
- It may have positive or negative charge.
- Electric charge is a feature of elementary particles. Charge of bulk ‘bodies’ is additive.
- The elementary charge is Cb.
- Elementary charge is a subject of electrical charge conservation law (which will be explained below).
- Electric charge is invariant to the reference system.
Charge conservation law states that the algebraic sum of all the charges is constant in electrically isolated systems. An electrically isolated system is a system where no charges are coming in or out.
Here we will consider electrostatics where considered charges and charged bodies are static.
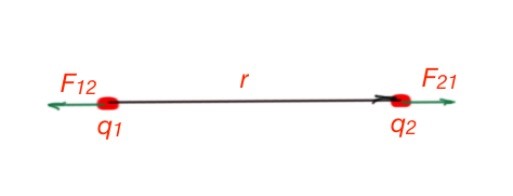
Based on the series of experiments by Charles Coulomb, Coulomb’s Law 1785 states that: the force of electrostatic interaction between two point charges is proportional to the multiplication of their charge modules and reversely proportional to the square of distance between them. This is force of repulsion for same sign charges, and attraction force for opposite charge signs. The formula illustrating Coulomb’s law can be seen in Figure below.
By Newton’s third law, particle 1 affects particle 2 with the same force as particle 2 affects particle 1, but in the opposite direction.
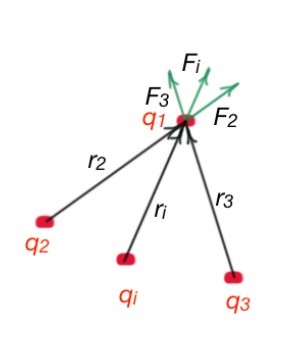
For all electrostatic interactions the principle of superposition states the following: the dot charge q1 is affected by several charges q2 … qn, and this affection can be considered as Coulomb force . Then the electrical effect of the group of these charges on the charge q1 is a force equal to the vector sum of forces (Figure below). It can be described by the formula .
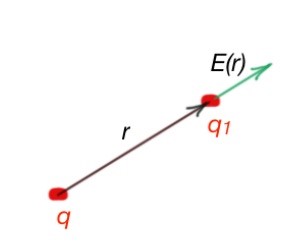
Let’s introduce the term of electric field. Electric field is a ratio of the electrostatic force, affecting the dot charge in the electric field, to the module of the value of this charge.
Let’s consider the Coulomb force affecting the charge from the system of charges charges. According to the superposition principle
We can see that electric field does not depend on the charge , which means it is a pure field characteristic. So if every dot in the area is determined, the area (or space) is determined, and states that the vector electric field is determined. The electric field is created by single dot charge .
The formula for Coulomb’s Law for a system of charges (above): or .
This is superposition principle for electric fields. To find the electric field created by ‘bulk’ charged objects, they have to divide the dot charges where we can apply the superposition principle.
Task 1: Prove that the electric field created by the charged sphere is
(Figure below).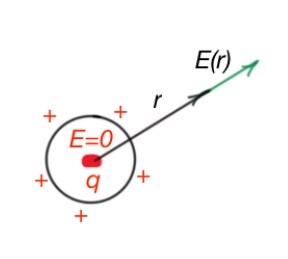
Electric fields can be illustrated with vectors from the dot charge (or bulk charged object) to every point in the space. As a result these vectors have to be summarised. It is easier to represent a field as some vectors of electric field, which can be prolonged to the infinite space.
These lines, which are tangent in every point of the electric field, coincide to the electric field vectors, and are called electric field lines. These lines help to determine direction and value of the electric field in every point of space. Figure 5 illustrates electric field for dot charge, for 2 dot charges with different signs, and for two planes. For planes, far from their edges, the electric field is considered as homogenous, and its lines are parallel to each other.
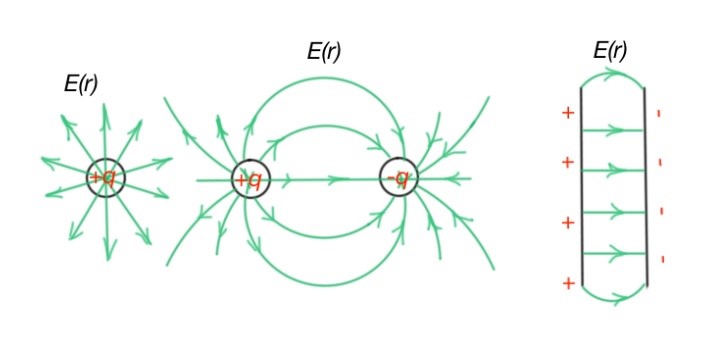
Lines of electric field have some features:
- They are not closed
- They are not overlapping
- The value of electric field is proportional to the density of electric field lines
Task 2: Find the electric field on the axis of a circle with radius R, where x is the distance from the centre of the circle. q – is the charge of the circle, using superposition principle and the formula for the electric field.
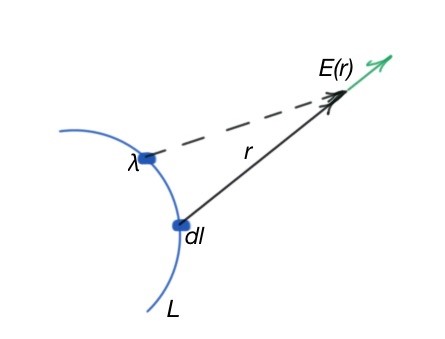
In complex cases of one-dimension charge distribution, we can use integration as the superposition principle. For example, if we have a linear object (Figure 6), the electric field can be found by the formula: where is the charge density for the object . In this case the object is linear, so charge density is linear also. In this case electric field vectors r ̅ are also different for every point of space. If the charge is distributed by the two- or three-dimension space, then we can use the terms of surface and volume charge density:
And the electric field for this case will be described by the following: , here – symbolises the surface and volume integrals.