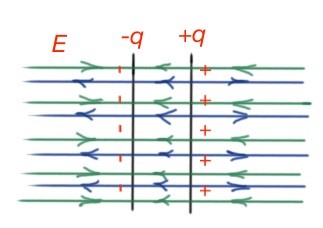
A capacitor is a system consisting of a two conductors, where an isolated electric field is created between two equal conductors , opposite charges. Isolated electric fields means all the electric field lines start at one conductor and end on the other conductor.
This may happen if the distance between conductors is very small compared to their dimensions. There are different types of capacitors in electronics. Figure 19. Capacitors are used to accumulate and store electric charge, energy and field.
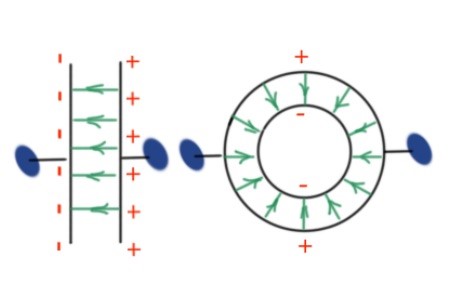
Capacitance is the ratio of capacitor charge to the potential difference between capacitor plates.
Potential difference between capacitor plates is .
This statement works for the electric field created by the charged capacitor plates. If the capacitor is isolated, then the electric field is determined only by capacitor geometry and charge of capacitor plates. And in every point of the field
And then
This means capacitance of a capacitor depends on the capacitor geometry and permittivity of a dielectric between capacitor plates ԑ. Let’s consider
which is a ration of capacitance of dielectric capacitor and capacitor without dielectric. Analytical forms of capacitance can be found only for simple forms of capacitors like plate, sphere and cylinder.
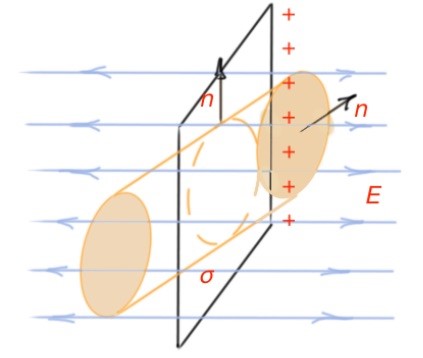
Let’s find the capacitance of a flat capacitor. Figure 19. First of all, let’s take away one capacitor plate, and consider the second plate as infinite and calculate the field for this capacitor plate only. Figure 20. Electric field flows through the cylindrical surface as the following:
– charge inside this surface is σS. Then according the Gauss theorem
And
This field is not dependent on any coordinates, so it is uniform.
Returning to the capacitor with parallel plates Figure 21, and equally but oppositely charged, we can see that the electric field exists only between the capacitor plates (according to the superposition principle).
– electric field outside the capacitor
– electric field inside the capacitor
where
In general cases flat capacitor capacitance is