Shift current and Maxwell equations

Variable magnetic fields create a vortex electric field in the conductor, which leads to the electric current appearance in the conductor. Let’s consider two cases. When we are talking about DC currents across a conductor, there is no need to consider special surface , enclosed with a contour. The same current goes through any surfaces we choose.

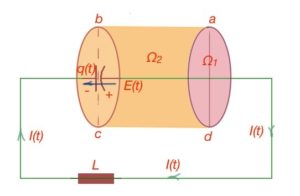
When we are talking about AC current through the conductor, the question of surface arises and circulation theorem becomes very important. (Figure 38). In this case, circulation theorem through the surface  gives the following:

$\int B_{r}dr={\mu }_0^{}{\int }_{\Omega 1} j_n^{}dS={\mu }_0^{}I$

According to the circulation theorem, we also can choose another surface , crossing the capacitor plates, for example. This surface will contain the charge, equal to the capacitor plate charge. The current through the surface

$\Omega \_2 is \frac{dq}{dt}$

In accordance to Gauss theorem

${\epsilon }_0{\int }_{\Omega }{E}_{n}dS=q$

Then the current through this surface is

$I={\epsilon }_0\frac{d}{dt}{\int }_{\Omega }{E}_{n}dS={\epsilon }_0{\int }_{\Omega }\frac{\partial E_n}{{\partial }_t}dS$

This current is called shift current, and

${\epsilon }_0\frac{\partial E_n}{{\partial }_t}$

is the shift current density.

Charges do not move between the capacitor plates, but we can see time variable electric field, that creates the magnetic field. So electric vortex fields create magnetic fields, and magnetic fields create electric vortex field.

The laws and theorems discussed here lead us to the set of Maxwell equations  – mathematical form of fundamental laws of electromagnetism:

$$\begin{gathered} {\int }_{\Omega }{E}_{n}dS=\frac{1}{\epsilon {\epsilon }_0}q \\ {\int }_{\Omega }{B}_{n}dS=0 \\ {\oint }_c E_{r}dr=–{\int }_{\Omega }\frac{\partial B_n}{{\partial }_t}dS \\ {\oint }_c B_r=\mu {\mu }_0({\int }_{\Omega } j_{n}dS+\epsilon {\epsilon }_0{\int }_{\Omega }\frac{\partial E_n}{{\partial }_t}dS) \end{gathered}$$