Elementary work of external forces to move charge dq in electric field of a capacitor
Total work is
this work determines total energy stored in a capacitor, Q is a total capacitor charge.
and energy of a charged capacitor
Let’s express these characteristics through the electric field parameters. For flat capacitors
and
then
V – is is the volume between capacitor plates. Therefore, volume energy density can be found for a capacitor
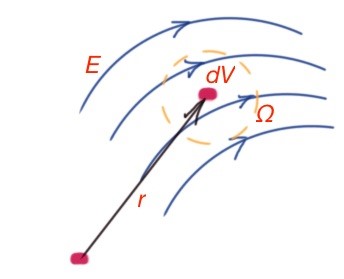
Volume energy density has local characteristics, and it corresponds to the piece of a capacitor where the electric field is uniform and equal to E. Let’s consider the term of volume energy density, on the example of non-uniform electric field. Take a piece of space with volume dV, that characterises radius-vector r. Volume density of energy in general is the value expressed by the formula
Figure 22 dWe is the energy of the small piece of electric field. So if we know the electric field E(r), we can calculate the energy of any piece of field with finite dimensions Ω. Therefore,
These formulas work for the uniform capacitor material with permittivity ε=const.
from negative to positive charge – called the dipole shoulder. Figure 23. For example, molecules
are dipoles. Let’s find out how dipoles behave in different kinds of electric fields.
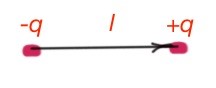
This means a uniform field turns the dipole along the field lines.
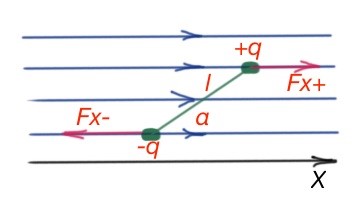
Then
Dipoles are oriented along the field. Fx has a positive or negative sign depending on the electric field, and if it is increasing or decreasing along the 0X axis. Dipoles are drawn into the stronger part of field. Electric field increment is
then the force affecting the dipole is
The conclusion is that dipoles are orienting along the electric field lines and drawing into the electric field with a bigger intensity.
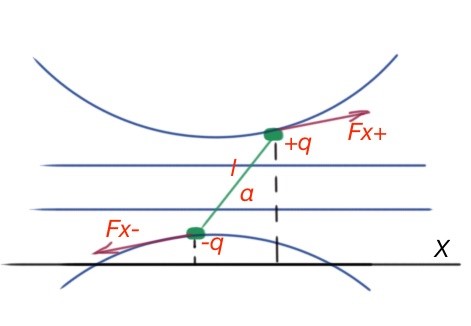
Dipole energy in the electric field
then
Force of electric field