Electronic filter

Electronic filters are four-terminal devices that serve to transfer electrical current between the source and load in a certain frequency range. The transparency range of the filter is the frequency range where the filter conducts without losses. The attenuation range of the filter is the frequency range where the filter conducts with attenuation.

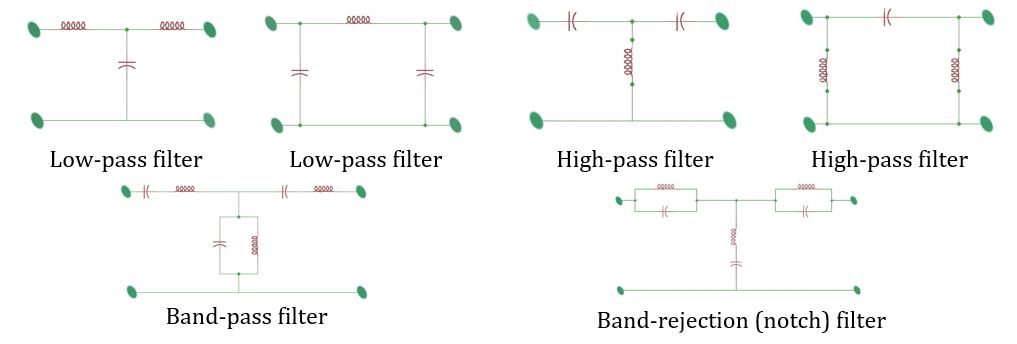
Electronic filters are used in radio applications and consist of capacitors, inductances and sometimes resistors. In high frequency applications the active part of the inductances and capacitances is usually neglected. The principal of filter construction is depicted on the figures below.

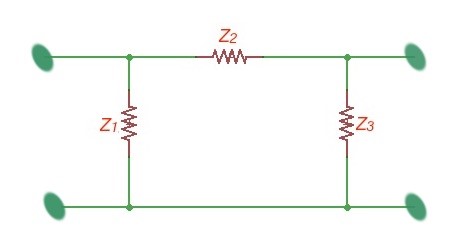
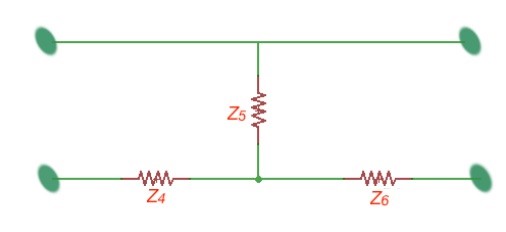
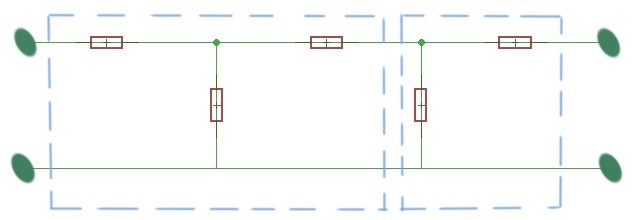
There is a term that exists called k-filters. These filters consist of a combination of the repeating section of filter units (depicted on the figures above), and as shown on further figure below. The load resistance should be matched to the filter resistance. The electrical filters are characterised with better quality if their attenuation is large in the attenuation frequency range.

The filtering characteristics of four-terminals are due to the resonance effects of current and voltage in four-terminals. If the load resistance is matched to the filter resistance, then the input current and voltage of the filter is related to the input current and voltage of the load. $U_L=U_f{e}^{-(a+\mathrm{bj})}, I_L=I_f{e}^{-(a+\mathrm{bj})}$.

Here the coefficient $e^{–a}$ shows the attenuation rate, the coefficient $e^{–jb}$ shows the phase shift. The border frequency between transparency and attenuation fields of a filter is called the cutoff frequency. If we change the work frequency ω, then the four-terminal coefficients will change too. So when changing the work frequency ω it is important to change the load resistance. The filter resistance in the transparency field is active, in the attenuation zone it is reactive.

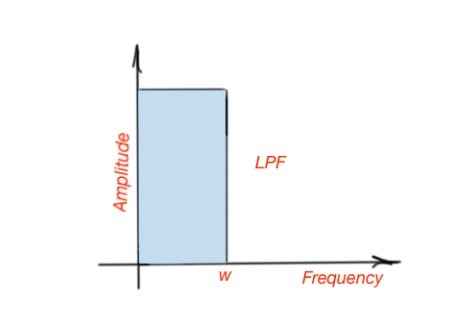
Low-pass filters (LPF) are those that are characterised with a transparency zone in the frequency rage from 0 to ω, and with an attenuation zone in the frequency range from $\omega$ to $\infty$. High-pass filters (HPF) are characterised with the transparency zone in the range $\omega$ to $\infty$, and attenuation zone from $0$ to $\omega$. Here the frequency $\omega$ is a cutoff frequency. The simple schemes of these filters are depicted below.

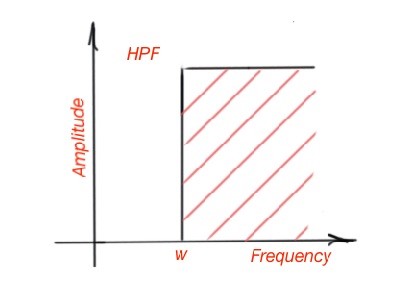
There are also filters that are characterised with transparent zones in the range of frequencies ${\omega }_1$ and ${\omega }_2$, the zones $0$ to ${\omega }_1$ and ${\omega }_2$ to $\infty$ are attenuation zones. These filters are called band-pass (BPF). The filters characterised with a transparent zone in frequency ranges $0$ to ${\omega }_1$ and ${\omega }_2$ to $\infty$, and attenuation zone from ${\omega }_1$ to ${\omega }_2$_, are called band-stop filters (BSF). The examples of band-pass and band-stop filters are depicted below.

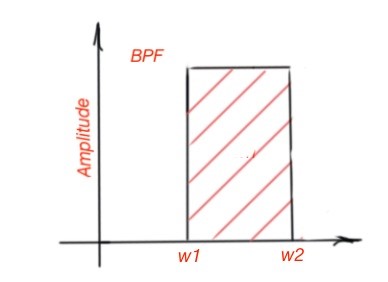
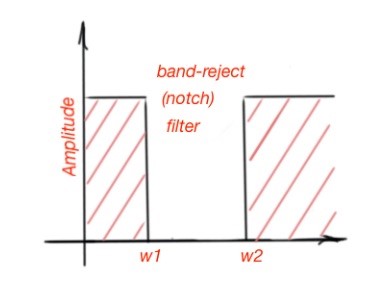
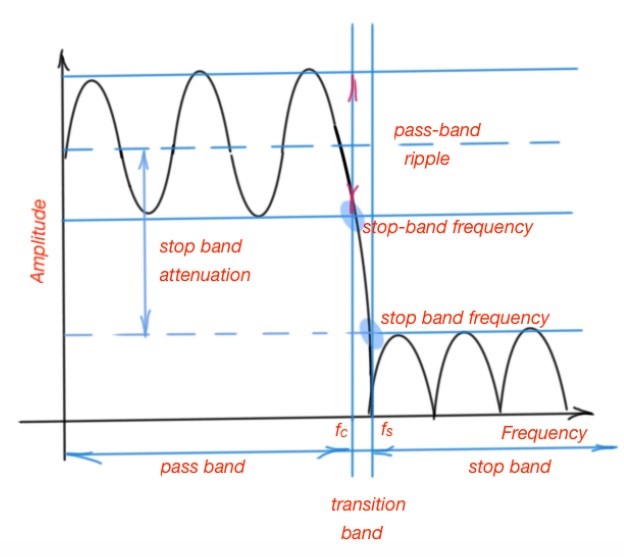
BPF can be made by cascading the HPF and LPF, and is characterised with lower cut-off frequency and upper cut-off frequency ($f_{LC}$ and $f_{UC}$). There is also a band-stop filter which can be characterised with lower and upper cut-off frequencies. A band-stop filter can also be called a band-reject or notch filter. A filter is characterised by the following parameters:

1. Cut-off frequency $f_C$, as mentioned above;
2. Stop-band frequency, $f_S$, that characterises the frequency where the minimum attenuation is achieved at the stop-band;
3. Minimal attenuation, $A_{min}$  is a minimal signal attenuation of the filter pass-band;
4. Pass band ripple $A_{max}$ , which is a variation of the pass band response;
5. $M$, the filter order, that defines the filter steepness.

As we know, filters consist of inductances and capacitances, and their response changes with frequency. So the corresponding impedances can be viewed as: $Z_L=\mathrm{sL}, Z_C=\frac{1}{\mathrm{sC}}$, here the s parameter is a complex frequency ?=?+??, where ? is the frequency (Np), and ? is the frequency (Rad).

The transfer equation for the filter in the most general form is: $H(s)=\frac{a_m{s}^m+...+a_0}{b_n{s}^n+\cdots +b_0}$.

Resolving this equation we can find the position of the roots on the s-plane (where imaginary components are vertical, and the real component is horizontal). If all the roots are on the left side of the plane, then the filter is stable. It helps us to work with two important parameters of the filters, that were mentioned above: $F_C$ cutoff frequency and , quality factor.

_{$F_C$} cutoff frequency  is a frequency where the filter response is down 3dB from the pass band. $Q$, quality factor describes the filter’s bandwidth relative to its centre frequency $Q=\frac{1}{\alpha }$. You can see the quality factor graphs in the Analog Devices datasheets, for example.

For filters, you will notice that if Q>0.707, then the filter response graph has a peak, if Q<0.707, the filter response is smooth. So what do these parameters mean? They play an important role in the definition of the transfer function and characterisation of the filter.

The transfer function for LPF is $H(s)=\frac{H_0}{s^2+{\omega }_0/Qs+{{\omega }_0}^2}, {\omega }_0=2{\mathrm{\pi F}}_C, H_0$ is an band-pass gain.

The transfer function for HPF is $H(s)=\frac{H_0{s}^2}{s^2+\frac{{\omega }_0}{Q}s+{{\omega }_0}^2}$ here ${\omega }_0=2\pi F_C$, $H_0$ is a band-pass gain.

The transfer function for BPF is $H(s)=\frac{H_0{{\omega }_0}^2}{s^2+\frac{{\omega }_0}{Q}s+{{\omega }_0}^2}. \mathrm{Here} \mathrm{the} \mathrm{gain} \mathrm{is} H_0=\frac{H}{Q},\mathrm{Q=}\frac{F_0}{F_H–F_L}$.

Here the quality factor $Q$, has a special meaning. The difference $F_H–F_L$ is a bandwidth. The $F_H$ and $F_L$ are the frequencies where the response is -3dB maximum. The band-pass filter can be narrow and wide. The narrow band-pass filter is a classical one. The wide band-pass filter can be made with the combination of high-pass and low-pass filters.

For the band-reject filter or narrow filter, the transfer function is $H(s)=\frac{H_0({{\omega }^2}_z+s^2)}{s^2+\frac{{\omega }_0}{Q}s+{{\omega }_0}^2}$, here ${\omega }_z$ is the zero frequency. The band-reject filter can also be narrow-band and wide-band. The narrow-band band-reject filter is called a notch filter, and the wide-band band-reject filter keeps it’s name. The relationship between ${\omega }_z$ and ${\omega }_0$ tells us about the type of the notch filter – it can be low-pass, standard and high-pass. If ${\omega }_z={\omega }_0$, then it is a standard notch filter. Low-pass notch filters occur when ${\omega }_Z>{\omega }_0$. A high-pass notch filter occurs when ${\omega }_Z<{\omega }_0$.

(«Theoretical basis of electrotechnics», L.A. Bessonov.; “Analogue filters”, Analog Devices.)

#8 Three-phase circuits