We know how to find the potential difference between two points in the electrostatic field:
Let’s find out the reverse dependence – electrostatic field , if we know potential difference two points in this field. Charge moves to the distance making work: and at the same time the definition of work . So and .
This means that field projection along the direction is equal to the potential rate between points and in the electrostatic field. “-” in the formula means that electric field has the same direction with decreasing potential . For Cartesian coordinate system
The electric field vector is :
or
Task : Determine the electric field on the axis of uniform charged circle with radius R. Its potential is known is a charge of the circle.
Conductors in the electric field
For simplicity, let’s consider the conductor as a metal. This conductor contains an enormous number of free charges, that are normally in the equilibrium state.
- The electric field in the conductor in the equilibrium is 0. Electric field in the conductor causes electric current, and free charges are ‘directly flowing’ only until the moment when the electric field will become 0.
- Field potential for all the points in the electric field is the same . This is a conclusion from the formula
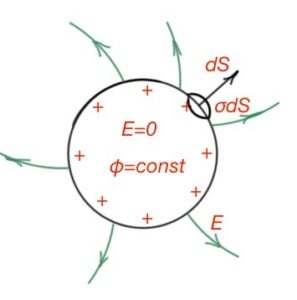
- Excessive charge in the conductor is distributed along the conductor surface. Total charge of the conductor is 0, (except the thin surface layer). This statement can be showed using the divergence theorem. At any point of the conductor so then .
- Electric field lines close to the surface of the conductor are perpendicular to the surface. Conductor surface is an equipotential surface.
- Electric field of a charged conductor close to its surface is proportional to the surface charge density. To show this statement, let’s take a cylindrical piece of a conductor with charge density σ. . Total charge inside the surface Then
6. Surface density of a conductor charge depends on the surface curvative. Let’s replace the real conductive body with its model, where minimal curvative is characterised by radius R1, maximum – R2. Then, having the following formulas for the charged system:
Then and . And according to divergence theorem
#4 Conductors in the external electric field. Faraday theorem