Usually electric circuit schemes appear complex where it’s not easy to find out parallel or serial connection for elements. Here below we will consider some techniques which will help us to simplify complex electric circuits, techniques are called and conversions.
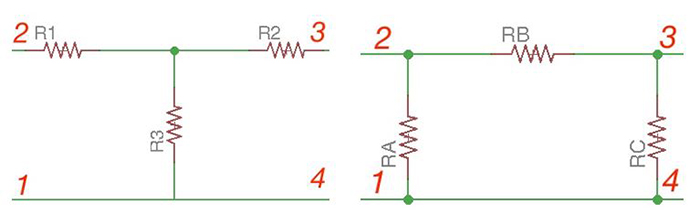
Figures 13 and 14 show or terminal network and or network. These networks can also be a part of larger network and can be used in electrical filters or 3-phase networks.
When we meet or network in a circuit, network can be superimposed on the latter to find the equivalent resistances.
Resistance between the same pair of nodes should be the same for both schemes. Let’s calculate resistance between terminals 1 and 2.
, means
Hence . Similarly and .
Rule: to conversion. Each resistor of network is equal to the product of adjacent resistances of network, divided by the sum of resistances.
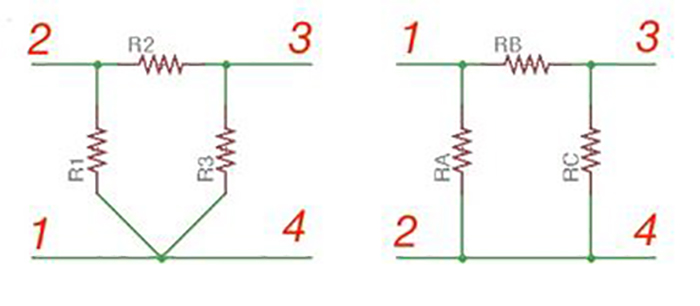
Delta-to-Wye conversion
To find the reverse conversion of resistances from network to , we must find the following sum:
thus
Rule: to conversion. Each resistor of network equal to the product of any possible pair of network resistors divided by the opposite network resistor.
The networks and are balanced when:
And .