LTI systems and their properties

This post covers properties of LTI system. Linear-time invariant systems, that were partially discussed before, play an important role in describing signals. Generally speaking, any process can be described with the idea of Linear-Time Invariant systems. So here we will consider LTI system properties in detail.

Let’s consider continuous-time function $f\left(t\right)$. We can divide it into fractions as depicted in Figure 1. Each fraction can be described with $\delta –$ function $\delta \left(t\right)=\left\{\begin{array}{l}\frac{1}{\tau }, 0<t<\tau \\ 0, t<0, or t>\tau \end{array}\right.$.

Let’s assume that $T\to 0$, then $f\left(t\right)={\int }_{–\infty }^{\infty }f\left(\phi \right)\delta (t–\phi )d\phi$. Let’s assume that $h\left(t\right)$ is the response of LTI system to the input $\delta –$function. So the LTI system output for the function $f\left(t\right)$ will be $g\left(t\right)={\int }_{–\infty }^{\infty }f\left(\phi \right)h(t–\phi )d\phi$.

This expression is called a convolution integral for a system. Convolution is the mathematical operation of obtaining the third function from two others, describing how one of the function changes the form of another. Convolution can also be written as $g\left(t\right)=f\left(t\right)*h\left(t\right)$.

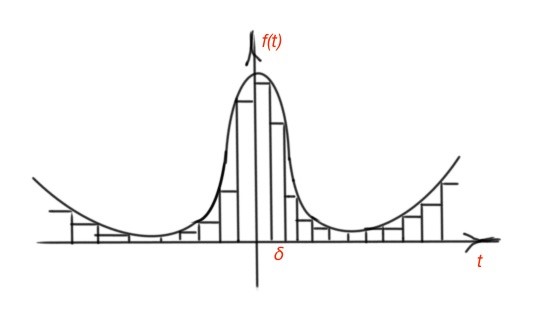
Figure 1.Continuous-time function represented with the impulses.

Let’s represent discrete-time signal as the row of unit impulses, as depicted in Figure 2. Mathematically it will be $f\left[n\right]=\sum _{k=–\infty }^{\infty }f\left[k\right]\delta \left[n–k\right]$ . As we know, $\delta –$function is the function equal to zero everywhere except zero. In our case, we can consider shifted $\delta –$function with weight $f\left[k\right]$ in every considered point. So here the considered function is a superposition of $\delta –$functions with corresponding weights.

Let’s assume that the LTI system response for $\delta –$function is $h\left[k\right]$, then the output function of the LTI system will be $g\left[n\right]=\sum _{k=–\infty }^{\infty }f\left[k\right]h\left[n–k\right]$. This expression is called a convolution sum for a system. Convolution is the mathematical operation of obtaining the third function from two others, describing how one of the function changes the form of another. Convolution can also be written as $g\left[n\right]=f\left[n\right]*h\left[n\right]$.

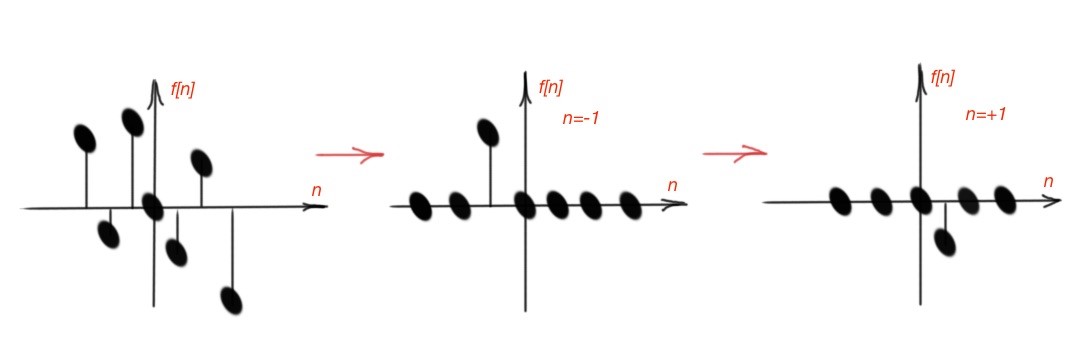Figure 2. The discrete-time function represented with impulses.

Here are some properties of linear-time invariant systems convolution.

1. Commutative property. For the input functions $f\left(t\right)$ and $f\left[n\right]$, and LTI system responses $h\left(t\right)$ and $h\left[n\right]$ the following expressions are valid:$f\left(t\right)*h\left(t\right)=h\left(t\right)*f\left(t\right)={\int }_{–\infty }^{\infty }f(t–\phi )h\left(\phi \right)d\phi$ and $f\left[n\right]*h\left[n\right]=h\left[n\right]*f\left[n\right]=\sum _{–\infty }^{\infty }f\left[n–k\right]h\left[k\right]$ .
2. Distributive property. For the input functions $f\left(t\right)$ and $f\left[n\right]$, and LTI system responses $h_1\left(t\right)$, $h_2\left(t\right)$ and $h_1\left[n\right]$, $h_2\left[n\right]$ the following expressions are valid: $f\left(t\right)*\left(h_1\right(t)+h_2(t\left)\right)=f\left(t\right)*h_1\left(t\right)+f\left(t\right)*h_2\left(t\right)$ and $f\left[n\right]*(h_1\left[n\right]+h_2\left[n\right])=f\left[n\right]h_1\left[n\right]+f\left[n\right]h_2\left[n\right]$.
3. Associative property. For the input functions $f\left(t\right)$ and $f\left[n\right]$, and LTI system responses $h_1\left(t\right)$, $h_2\left(t\right)$ and $h_1\left[n\right]$, $h_2\left[n\right]$ the following expressions are valid:$f\left(t\right)*\left(h_1\right(t)*h_2(t\left)\right)=\left(f\right(t)*h_1(t\left)\right)*h_2\left(t\right)$, and $f\left[n\right]*(h_1\left[n\right]*h_2\left[n\right])=(f\left[n\right]*h_1\left[n\right])*h_2\left[n\right]$.
4. Inversion property. If the LTI system is an inverting function, then $h_1\left(t\right)*h_2\left(t\right)=\delta \left(t\right)$ and $h_1\left[n\right]*h_2\left[n\right]=\delta \left[n\right]$, here $h_1\left(t\right), h_2\left(t\right), h_1\left[n\right], h_2\left[n\right]$ are responses of the input and output functions in the case of continuous-time and discrete-time functions.
5. Stability property. Let’s assume that the input function is limited, so $\left|f\left(t\right)\right|<A, \left|f\left[n\right]\right|<B$, then considering the convolution sum and integral we can understand if the output function is stable. $\left|g\left(t\right)\right|<{\int }_{–\infty }^{\infty }A\left|h\left(\phi \right)\right|d\phi$, so the output function $g\left(t\right)$ will be stable if the integral ${\int }_{–\infty }^{\infty }\left|h\left(\phi \right)\right|d\phi <\infty$. Similarly we can show for the discrete-time function $\left|g\left[n\right]\right|<\sum _{k=–\infty }^{\infty }B\left|h\left|k\right|\right|$ is stable if the sum $\sum _{k=–\infty }^{\infty }\left|h\left|k\right|\right|<\infty$. [1]

More educational tutorials can be accessed via Reddit community r/ElectronicsEasy.

 

[1] “Signals and systems”, 2nd edition, 1997. Alan V. Oppenheim, Allan S. Willsky.