Nodal method - Kirchhoff's Law. Circuit fundamentals

The idea of this nodal method is to find voltages of the nodes using the first Law of Kirchhoff, concerning the reference (ground) node. These voltages are nodal voltages, its positive direction is from the considering node to reference node.

The voltage of the branch is equal to the subtract of node voltages of the considering nodes, it’s composition with complex conductivity of the considering branch is the current of this branch. It means that the nodal voltages at the nodes are known, and we can determine the current of these branches.

Let’s take the third node as a reference (or ground) one – on the figure in the previous post , 1 and 2 – two other nodes, with node voltages $V_{1}$ and $V_{2}$ .

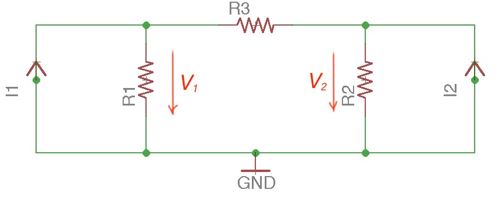
Circuit Fundamentals - Fig23 — Figure 23

According to the first Law of Kirchhoff, there will be the following equations:

I_{1} = G_{1} V_{1} + G_{3} (V_{1} - V_{2}) = (G_{1} + G_{3}) V_{1} - G_{3} V_{2}; I_{2} = G_{2} V_{2} + G_{3} (V_{2} - V_{1}) = (G_{2} - G_{1}) V_{2} - G_{3} V_{1};

Conductancies of the branches converging in the node, shared with the reference node, are intricate conductancies – conductancies shared between two nodes are shared conductancies. If currents of current sources and conductancies are known, then node voltages can be found by solving the equations system:

\{\begin{cases}  \end{cases} \begin{matrix} I_{1} = G_{11} V_{1} + G_{12} V_{2} + . . . {G_{1}}_{(q - 1)} V_{q - 1} \\ I_{2} = G_{21} V_{1} + G_{22} V_{2} + . . . G_{2 (q - 1)} V_{q - 1} \\ I_{q - 1} = {G_{(q - 1)}}_{1} V_{1} + G_{(q - 1) 2} V_{2} + . . . G_{(q - 1) (q - 1)} V_{q - 1} \end{matrix}

Conductancies G_ii intricate conductance of the branches converging in the node i, G_ikis shared conductance between nodes i and k (it goes with “-“ in the equation). Currents of the sources coming into the node are with “+” , coming out from the node are with “-“.

Resolving this system of equations we will get the following formula for nodes voltage:

V_{i} = \frac{1}{∆_{G}} \sum_{k = 1}^{q - 1} I_{k} ∆_{k}, ∆_{k} = |\begin{matrix} G_{11} G_{12} . . . G_{1 (q - 1)} \\ G_{21} G_{22} . . . G_{2 (q - 1)} \\ G_{(q - 1) 1} G_{(q - 1) 2} . . . G_{(q - 1) (q - 1)} \end{matrix}|

These equations are constructed with the idea of current sources. If the circuit contains voltage sources they should be replaced by the equivalent current sources. If there are some branches with only EMFs, they can be taken into account as unknown currents and excluded, because their conductivity is a big infinity. If there is only one branch with EMF in a circuit with infinity big conductivity, then the reference node can be as one with this branch node. It will decrease the number of variables in the equation system.

The nodal method is more preferable then the mesh method when the number of nodes is much less than the number of branches.

Superposition principle

Kirchhoff’s Law – nodal method

Leave a Reply Cancel reply