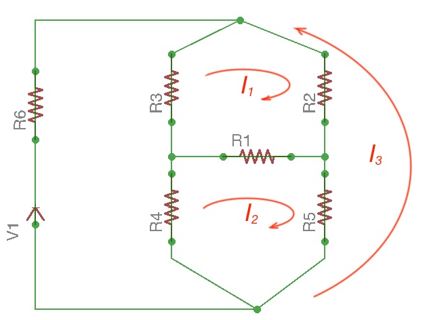
The idea of this mesh method is calculating mesh currents of meshes (closed loops in a circuit), instead of the currents of branches, using second Kirchhoff’s Law. There is 2 loop schemes in Figure 18 (article 10), and the chosen loops are meshes. and are chosen mesh currents. There current that goes through resistor , current goes through resistor , current goes through the resistor , as and currents are directed opposite.
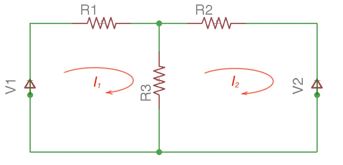
According to the second Kirchhoff’s Law, the number of equations is equal to the number of meshes. Consider all the parameters are complex ones for synthesis of the technique. Consider also that the sum of complex resistances of the meshes as intrinsic resistance of the mesh, sum of complex resistances common for both meshes as shared resistance of the meshes. For the network in Figure 18 we have the following equations according to the second Kirchhoff’s Law:
Here and – intrinsic resistance, – is common resistance.
If the network has n meshes, then having n equations according to the second Kirchhoff’s Law:
Here – intrinsic resistance of the mesh, – shared resistance of the meshes, – emf of the mesh ( – with a positive sign if its direction matches with the mesh current direction, with negative if it is the other way).
The solution of this equation system can be found by the following matrix determinants:
Finally the equations system for mesh currents is the following:
– algebraic complement of an element of matrix determinant.The abbreviated equation system is the following:
is a mesh number, which corresponds to the EMF we are multiplying by the algebraic complement; k is a mesh number of the mesh current we are calculating.
The equations above are proposed if there are voltage sources in a circuit. In the case that there are current sources in the circuit, these currents can be taken as mesh circuits, and the quantity of unknown mesh circuits will be less to determine. If there are parallel branches in the circuit, replacement of these resistances by equivalent ones will reduce the quantity of equations.
Electric circuits can be planar and non-planar. Planar electric circuits can be drawn with uncrossed branches. Non-planar electric circuits can not be drawn with uncrossed branches.
If the direction of mesh currents is similar for all meshes (clockwise or counterclockwise for all meshes), the shared resistances appear negative in the equation (1), because mesh currents for this resistance are oppositely directed.
Example 1.
Find the current of the resistor on the figure below.