How to calculate power and energy in RC circuit

This post describes how to calculate power and energy in RC circuit. Energy consumption and power dissipation are very important characteristics of the digital circuit.

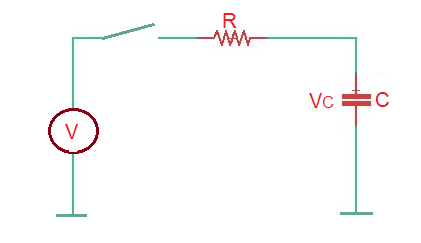
Let’s consider the simple RC circuit with the voltage source as depicted below.

From the previous posts we know that power delivered to a circuit element is $p (t) = v (t) i (t)$ . Resistor and capacitor perform different functions in terms of the power in the circuit: resistor – dissipates energy, and capacitor – stores energy.

So the instantaneous power from the source is $p (t) = V i (t)$ . Current here is $i (t) = \frac{V - v_{C} (t)}{R}$ . We already know that for this circuit capacitor voltage is $v_{C} (t) = V (1 - e^{- \frac{t}{R C}})$ . Then we have for power $p (t) = \frac{V^{2}}{R} - \frac{V^{2}}{R} (1 - e^{- \frac{t}{R C}}) = \frac{V^{2}}{R} e^{- \frac{t}{R C}}$ .

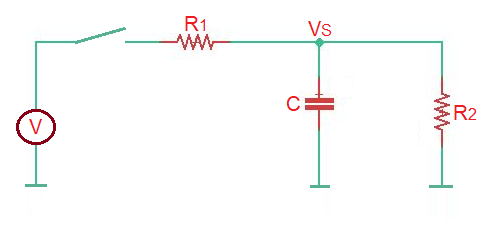
Then we can find that energy supplied by the source $ω = \int_{0}^{T} p (t) d t$ if $T = \infty$ , then supplied energy is $ω = C V^{2}$ . Energy stored by capacitor is $ω_{C} (t) = C \frac{V^{2} (t)}{2} = \frac{C V^{2}}{2}$ . Instantaneous power on the resistor is $p (t) = R i {(t)}^{2} = \frac{V^{2}}{R} e^{- \frac{2 t}{R C}}$ . In order to find the energy dissipated by the resistor is $ω = \int_{0}^{\infty} \frac{V^{2}}{R} e^{- \frac{2 t}{R C}} d t = \frac{C V^{2}}{2}$ .

Let’s consider the circuit with the switch, that gives the step signal, depicted below.

So here we have two situations here – when capacitor is charges and when capacitors is discharges. It charges from the source when the switch is closed, while resistors $R_{1}$ and $R_{2}$ are dissipating energy. When the switch is opened, capacitor discharges via the resistor $R_{2}$ .

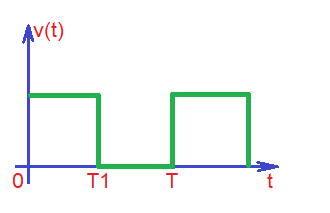
The average power is the total amount of energy dissipated during certain interval of time, divided by the length of the time interval $T$ , i.e $p = \frac{ω}{T}$ . Where $ω (t) = \int_{0}^{T} p (t) d t$ .

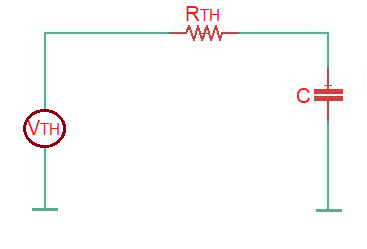
When the switch is on, we can transform the circuit using the Thenevin theorem, we have the following equivalent circuit:

Here $V_{T H} = \frac{V R_{2}}{R_{1} + R_{2}}$ , and $R_{T H} = \frac{R_{1} R_{2}}{R_{1} + R_{2}}$ . As we considered before the total solution in this case will be the sum of the homogeneous solution and particular solution.

The homogeneous solution here is $v_{C} (t) = V_{T H} (1 - e^{- \frac{t}{C R_{T H}}})$ . The total power dissipated by the resistors will be a sum of power dissipated on resistor $R_{1}$ and $R_{2}$ . In this case we have $p (t) = (V - v$ _C)2R1+vC2R2, where $v_{C} = V_{T H} (1 - e^{- \frac{t}{C R_{T H}}})$ .

Using the formula for power we can find energy dissipated in the circuit during period of time $0 \to T_{1}$ is $ω_{0 \to T 1} = \int_{0}^{T_{1}} (\frac{{[V - V_{T H} (1 - e^{- \frac{t}{C R_{T H}}})]}^{2}}{R_{1}} + \frac{{[V_{T H} (1 - e^{- \frac{t}{C R_{T H}}})]}^{2}}{R_{2}}) d t$ . After simplification and rearrangement we have $ω_{0 \to T_{1}} = \frac{V^{2}}{R_{1} + R_{2}} T_{1} + \frac{{V^{2}}_{T H} C}{2}$ .

During the time interval $T_{1} \to T_{2}$ the switch of the circuit opens, capacitor discharging and resistor $R_{2}$ dissipates energy. Right at the start voltage of the capacitor is $V_{T H}$ . Capacitor voltage will change with time by the formula $v_{C} (t) = V_{T H} e^{- \frac{t}{R_{2} C}}$ .

Instantaneous power dissipated in the circuit $p (t) = v_{C} \frac{v_{c}}{R_{2}} = \frac{{V_{T H}}^{2}}{R_{2}} e^{- \frac{2 t}{R_{2} C}}$ , energy here is $ω_{T_{1} \to T_{2}} = \int_{T_{1}}^{T_{2}} p (t) d t = \frac{C {V^{2}}_{T H}}{2} (1 - e^{- \frac{2 T_{2}}{C R_{2}}}) \approx \frac{C {v^{2}}_{T H}}{2}$ .

The total dissipated energy is the sum of $ω = ω_{0 \to T_{1}} + ω_{T_{1} \to T_{2}} = \frac{V^{2}}{R_{1} + R_{2}} T_{1} + {v^{2}}_{T H}$ . The average dissipated power during period of time $T = T_{1} + T_{2}$ is $\bar{p} = \frac{ω}{T} = \frac{V^{2}}{R_{1} + R_{2}} \frac{T_{1}}{T} + \frac{{v^{2}}_{T H}}{T}$ .

The average power can be divided to static and dynamic power: $p_{s t a t i c} = \frac{V^{2}}{(R_{1} + R_{2})} \frac{T_{1}}{T}$ , $p_{d y n a m i c} = \frac{C {v^{2}}_{T H}}{T}$ .

Educational content can also be reached via Reddit community r/ElectronicsEasy.