Polarization is a dielectric state when every unit of a dielectric volume has its electrical moment. There are two types of polarisation – occurring in the electric field, and spontaneously. In some cases mechanical stresses can also cause polarisation. The dielectric constant is a parameter, characterising the ability of some materials to polarise.
is a dielectric capacitance of the medium, is a vacuum dielectric capacitance.
Polarization is followed by coherent charges on the surface of a dielectric. These coherent charges decrease the electric field inside dielectric. Polarity is quantitatively characterised by dielectric polarisation.
Polarity is a vector quantity, measured with
Polarity of homogenous flat dielectric in the uniform electric field is equal to the quantity of coherent electric charges. For most dielectrics, polarity is described by the following:
X is a dielectric’s susceptibility. For isotropic structures vectors P and E are directed the same. For anisotropic – P and E are tensor quantities. In the intense electric field P and E quantities are not linear, so non-linear effects occur in these conditions.
Capacitance of a capacitor with dielectric and accumulated charge, is defined by a variety of different mechanisms. Electronic polarisation is an elastic displacement and an electron orbits deformation in atoms and ions. Setting time for electronic polarisation is ~10-15, so this polarisation can be considered as instantaneous. Electronic polarisation is inherent to all dielectrics. For dielectrics, characterised with only electronic polarisation, the dielectric constant is equal to the square of light refraction index.
Electronic polarization is not dependent on the temperature, and the dielectric constant decreases when the temperature rises. This is because of the dielectric thermal expansion. The thermal factor of dielectric constant is:
Ionic polarization occurs in solid dielectrics with ionic structure, and is related to elastic displacement of ions in the lattice to the distances less than the lattice period.
Ion shift is hindered by the elastic forces of chemical bonds in a lattice. For the equilibrium qE = kΔx, k, is an elastic force coefficient, Δx is ion shift in the electric field.
There is an electric moment that occurs for two oppositely charged shifted ions:
So ionic impact into dielectric polarisation is considered by the total sum of all electric moments in the compound. When temperature rises the distance between ions increases, and elastic forces are weakened. This leads to the growth of polarisation.
Dipole-relaxation polarisation is characterised by partial orientation of dipoles, in the chaotic thermal movement, by the electric field. Dipole-relaxation polarisation occurs when molecular bonds are not hindering dipole orientation. Raising the temperature weakens the molecular bonds, so dipole-relaxation polarisation grows. However, the thermal movement of molecules is growing, and it weakens the orientation ability of the electric field.
Dipole movement requires overcoming of some compound resistance. So, dipole-relaxation polarisation is related to some energy losses and heating the dielectric. Dipole-relaxation polarisation is inherent mostly to polar liquids, and to some polar organic solids. Ionic-relaxation polarization is inherent to some non-organic glasses and some crystalline structures with no dense ions package.
In this case weakly bonded ions shift along to the electric field to distances bigger than the lattice period. When the electric field turns off, ions return to the lattice nodes. Electronic-relaxation polarization occurs due to excited electrons of dielectric structure defects. Resonant polarization occurs in dielectrics with light frequencies. It is related to physical and chemical properties of the dielectric.
ɛ change with frequency is a dielectric dispersion. Relaxation dispersion is characterised by monotonous decreasing of dielectric constant with raising frequency. For resonant dispersion dielectric constant rises and then falls at high frequencies. Migration polarization occurs in solids of non-homogenous structure with impurities and defects. This type of polarisation is related to huge electric energy dissipation. Spontaneous polarization is inherent to solids like ferroelectrics.
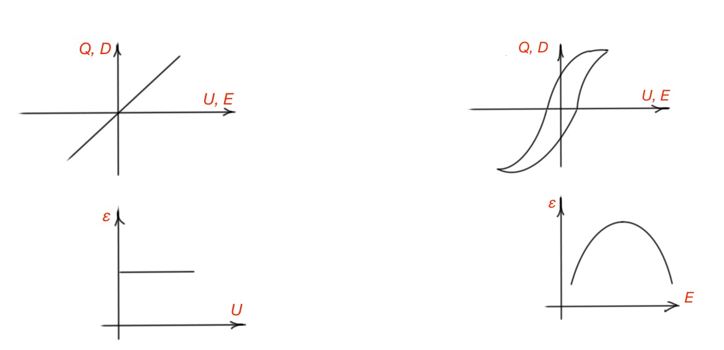
All dielectrics are divided to linear and non-linear dielectrics depending on the way of the dielectric constant reaction to external electric fields. Figure 28 illustrates the way of dielectric charge dependence on the voltage. Linear dielectrics are also divided by polar and non-polar. Polar dielectrics are organic liquid and solid dielectrics, characterised by dipole-relaxation and electronic polarisation.
Non-polar dielectrics are gases, liquids and solids in crystalline and amorphous forms, and are characterised by electronic polarisation. Ionic compounds are non-organic dielectrics, characterised by ionic, electronic, ionic-relaxation and electronic-relaxation polarisation. Dielectric constant depends on the state of substance. Gases have a rather small density due to the large distances between molecules. Due to this fact, their polarisation is rather small and their dielectric constant is close to 1.
Gas molecules are characterised by electronic or dipole types of polarisation. The bigger gas molecule radius, the bigger dielectric constant for gas, and it is proportional to the square of gas refraction index. Liquid dielectrics can consist of polar and non-polar molecules. For non-polar liquids dielectric constant is considered by electronic polarisation, proportional to the square of refraction coefficient – less then 2.5. Dielectric constant for polar liquids is more complex. Frequency plays a greater role at the dielectric constant for polar liquids. Figure 29 illustrates temperature and frequency dependence of dielectric constant.
Dielectric constant of solids can have different values depending on its structural features. Solid dielectrics with ionic lattice are characterised by ionic and electron polarisation, and their dielectric constant can have different values. Dielectric constant of non-organic glasses, similar to amorphous structures, may vary from 4 to 25. Solid polar organic dielectrics are characterised by dipole-relaxation polarisation.
Their dielectric constant to a greater extent depends on temperature and voltage frequency, as for dipole liquids. The dielectric constant of complex non-interactive components with different dielectric constants, can be presented with the Lihteneker formula:
are dielectric constants of components. are volume concentrations of components, and is the value.
Characterising components distribution in a compound, can be -/+1. Dielectric constant for these kinds of compounds can look like the following:
or the most frequent .
As an exercise, determine the temperature coefficient for dielectric constant of complex solid compounds: