Two-terminal networks in the AC circuit

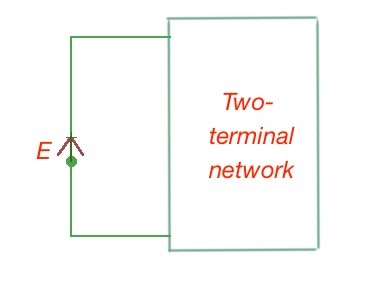
Let’s consider a passive two-terminal network, connected to the input source  $E$.

The input resistance in this case is $Z_{in}=\frac{E}{I}, Z_{in}=R_{in}+j{X}_{in}$, the input conductance is $Y_{in}=\frac{1}{Z_{in}}$. If the $X_{in}<0$, then the two-terminal network is capacitive, if $X_{in}>0$, then the two-terminal network is inductive.

The input resistance can be calculated in two ways – measurements and by calculating the circuit of the two-terminal networks. The first way is easier as you need only an ammeter, voltmeter, wattmeter and phasemeter, where you will need to check the angle between current and voltage.

A two-terminal network can work in the resonance regime. When the two-terminal network has few capacitance and few inductance, and the input resistance is active, then the two-terminal network is in the resonance regime. It’s current and voltage has the same phase and the reactive power is zero. Resonance regimes of the two-terminal network can be two types – current resonance and voltage resonance.

Current resonance, is the phenomena that happens in the circuit with different kinds of parallel resistances. Figure 2 depicts two parallel branches of the two terminal networks with different types of resistances. The first line is characterised with active resistance $R_1$ and reactive resistance $\frac{1}{\omega C}$, and the second parallel line is characterised with active resistance $R_2$ and reactive resistance $\omega L$.

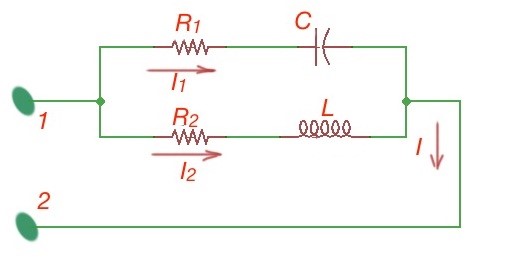
Current $I_1=U(g_1–j{b}_1)$, current $I_2=U(g_1–j{b}_1)$, current $I=I_1+I_2=U(g_1+g_2)–Uj(b_1+b_2)$. The definition of resonance states that the phase of the current should be equal to the phase of the voltage, i.e. $b_1+b_2=0$. Then $\frac{\omega L}{(\omega L{)}^2+R_1^2}–\frac{{\displaystyle \frac{1}{\omega C}}}{(\frac{1}{\omega C}{)}^2+R_2^2}=0$.

When the $R_2=0$  and $R_1\ll \omega L$, the resonance condition is ${{\omega }_0}^{2}LC\approx 1$, ${\omega }_0$ is the resonance frequency. This is a very particular case. Generally speaking we can obtain the resonance, changing the $L, C, \omega , R_1, R_2$ quantities.

Input resistance of the most consuming power devices is inductive. In order to decrease the consuming current, you will need to decrease the reactive constituent, the network of capacitance should be connected in parallel to the consuming device. In this case we can decrease the phase shift between the voltage and current of the power consuming device. This effect is called the phase shift compensation. This effect is very significant for high consumption systems.

Resonance of the voltages is the resonance in the scheme of the series $R, L, C$  components. Let’s consider the circuit on the figure below. To obtain the resonance the current phase should be the same as the voltage phase in the circuit, so the input resistance $Z=R+j(\omega L–\frac{1}{\omega C})$ will be active and the ${\omega }_{0}L=\frac{1}{{\omega }_{0}C}$, ${\omega }_0$ is the resonance frequency. The resonance voltage of the capacitor is equal to the resonance voltage of the inductance, so $U_L=\frac{{\omega }_{0}L}{R}E$. The parameter $Q=\frac{{\omega }_{0}L}{R}=\frac{\sqrt{{\displaystyle \frac{L}{C}}}}{R}$ is called the $Q$-factor of the electric circuit.

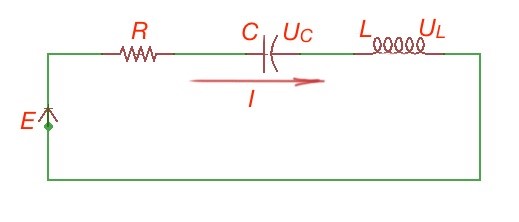
Characteristic resistance of the circuit is the ratio of the resonance voltage of the inductance or capacitance of the resonant current  $QR$.

Let’s consider the case when $E, R, L, C$ parameters are constant in the electric circuit and we can only change the frequency $\omega$. So the current in the circuit is $I=\frac{E}{\sqrt{R^2+(\omega L–{\displaystyle \frac{1}{\omega C}}{)}^2}}=\frac{{\displaystyle \frac{E}{R}}}{\sqrt{1+Q^2(\frac{\omega }{{\omega }_0}–\frac{{\omega }_0}{\omega }{)}^2}},U_L=\omega LI=E \frac{{\displaystyle \frac{Q\omega }{{\omega }_0}}}{\sqrt{1+Q^2(\frac{\omega }{{\omega }_0}–\frac{{\omega }_0}{\omega }{)}^2}}$, here ${\omega }_0$ is a resonance frequency. There are three cases:

1. $\omega \to 0$, then $X\to \infty$ and $I\to 0, U_L=0$
2. $\omega \to \infty$, then $X\to \infty$ and $I\to 0, U_L\to E$
3. $\omega =\frac{1}{\sqrt{LC}},$then $X=0$ and $I=\frac{E}{R}, U_L=\frac{E}{R}\sqrt{\frac{L}{C}}$.

Making a similar calculation, you can obtain the $U_C$  capacitor voltage ratings. When the frequency $\omega =\frac{1}{\sqrt{LC}}$ voltages $U_L$ and $U_C$ achieve their maximum ratings. We must note that the lower active resonance of the circuit, the higher it’s $Q$ -factor. The curve $Q\left(\omega \right)$ is depicted on the figure below.

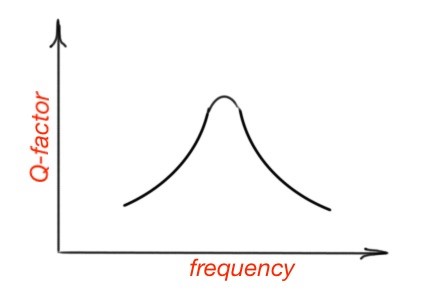
The bandwidth of the resonance circuit is the frequency band ${\omega }_2–{\omega }_1=\frac{{\omega }_0}{Q}$, the border frequencies ${\omega }_{1,2}=\frac{{\omega }_0}{2Q} (\sqrt{1+4Q^2}\pm 1)$, and the phase $\phi =–arctQ(\frac{{\omega }_0}{\omega }–\frac{\omega }{{\omega }_0})$.

So we can see the frequency characteristics of two-terminal networks. Input resistance and conductance are frequency dependent functions. And frequency characteristics of the two-terminal networks are the frequency dependence of the input resistance module and the frequency dependence of the real and imaginary parts of the input resistance. In general, two-terminal networks can contain resistive and reactive components. If the two-terminals contain only reactive components, it is called a reactive two-terminal.

Equivalent two-terminal network