Why filter is used in rectifier

Rectifiers are used for creating the smooth DC output voltage, for this purpose there is usually filters are used in rectifiers. This systems can be divided as inductor-input DC filters and capacity-input DC filter. Inductor-input DC filter is used in high-power applications, capacitor-input DC filters are used in relatively-low power applications.

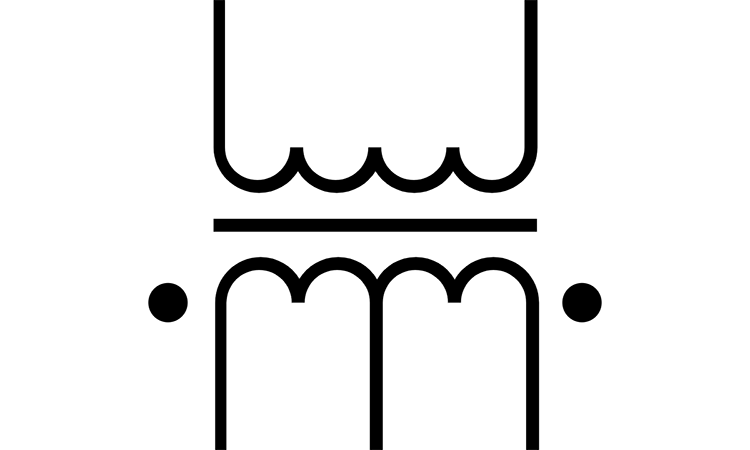
Inductive-input DC filters

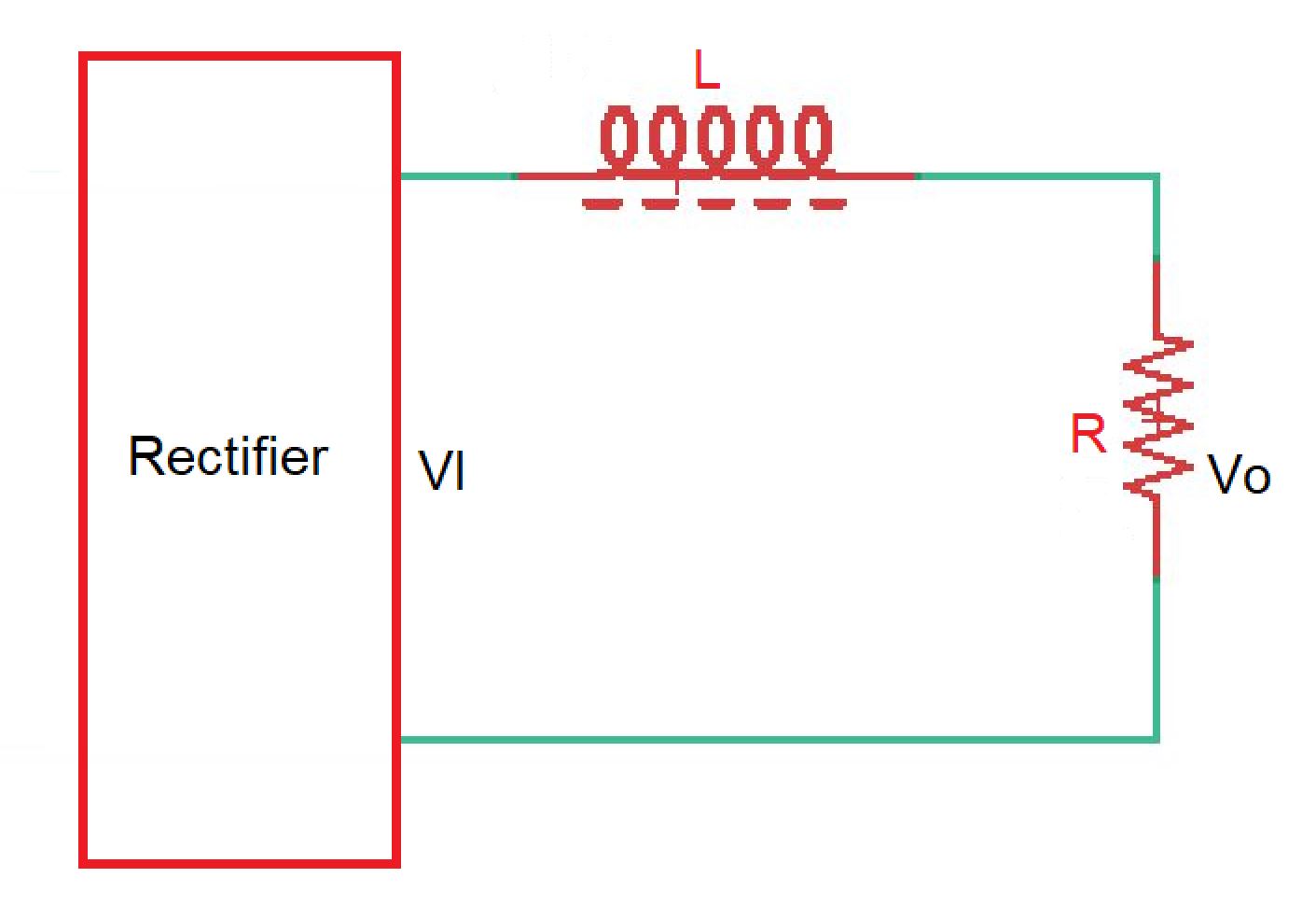
The inductive-input DC filters are depicted on the figure below. If the induction $ω L ≫ R$ , then rectifier output current is stable.

For simple inductor-input DC filter ripple can be reduced by the factor $\frac{R}{\sqrt{R^{2} + {(2 π f_{L} L_{f})}^{2}}}$ or $\frac{v_{0}}{v_{L}}$ , here $v_{0}$ is the ripple voltage after filtering and $v_{L}$ is the ripple voltage before filtering.

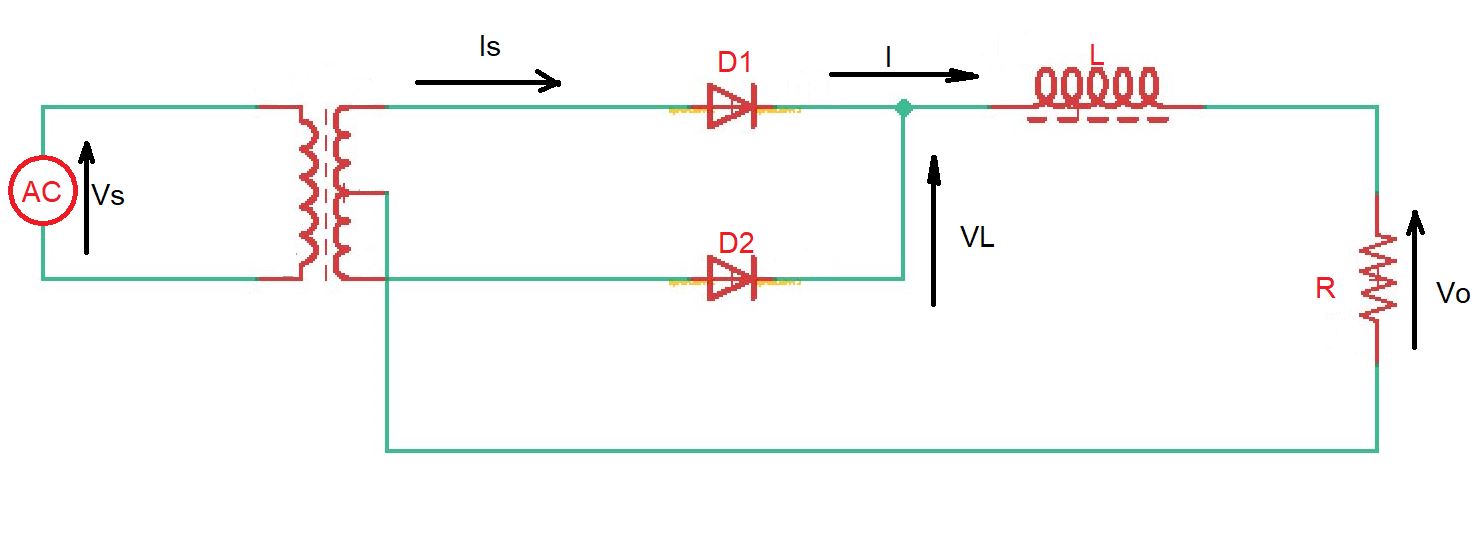
Here below you can see the full-wave rectifier with inductor-input DC filter.

Inductance in the circuit plays important role, as if inductance is finite, the output voltage and current through the inductor have ripple component, if the inductance is infinite – output current and voltage are constant. The minimal inductance value, called critical inductance $L_{C}$ , required for maintaining continuous current. For single-phase full-wave rectifier the critical inductance $L_{C} = \frac{R}{6 πf}$ , where $f$ is an input frequency.

Current and voltage characteristics for for full-wave inductor-input DC rectifier for finite and infinite inductance are depicted below.

Usually the choice of inductance depends on the required output voltage ripple factor. Ripple voltage without filtering is $v_{L} = - \frac{4 V_{m}}{π (n^{2} - 1)}$ , where $n = 2, 4, 8 . . .$ The ripple factor $R F = \sqrt{2 \underset{n = 2, 4, 8 . . .}{\sum {(\frac{1}{n^{2} - 1})}^{2}}}$ .

Total input distortion of the input current is $T H D = \sqrt{{(\frac{I_{S}}{I_{s 1}})}^{2} - 1}$ , here $I_{S}$ and $I_{s 1}$ are RMS and input current values. Input power factor is $P F = \frac{I_{s 1}}{I_{s}} \cos φ$ , here $φ$ is an angle between input current and voltage.

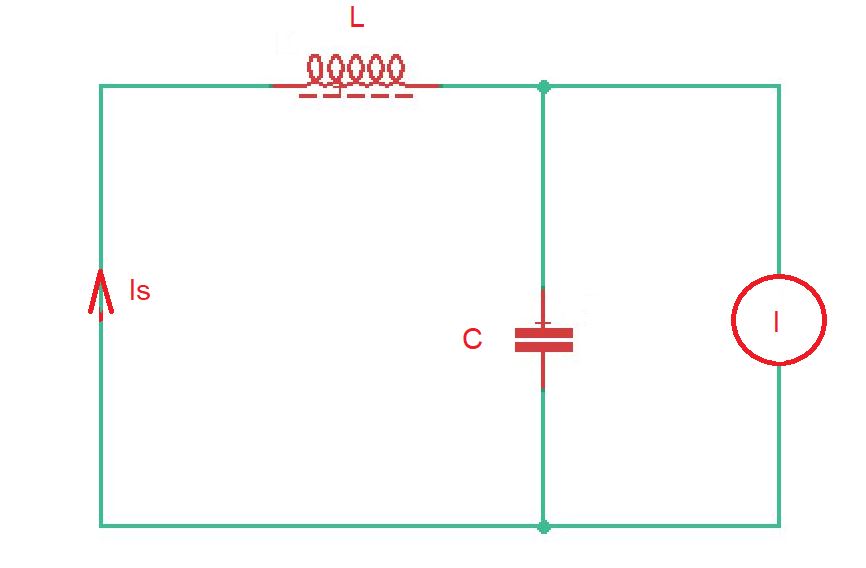
Figure below shows the rectifier with an input AC filter.

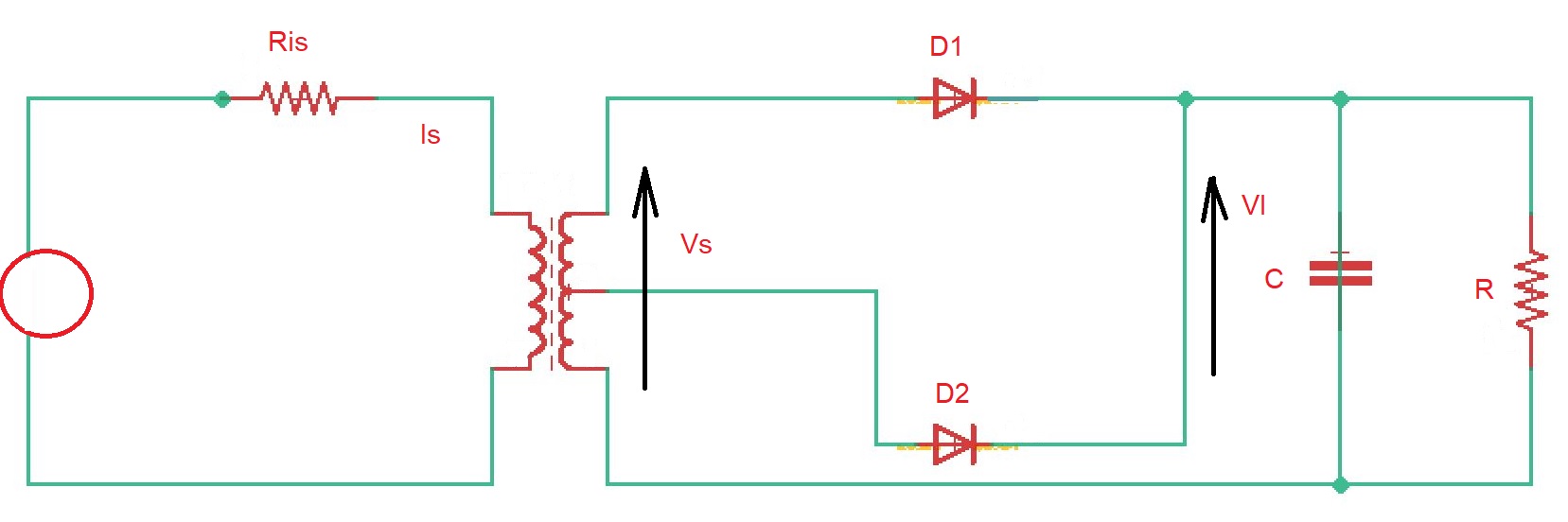
RMS value of the n-th harmonic of current is $I_{S} = I |\frac{1}{1 - {(2 n πf)}^{2} L C}|$ , where $I$ is RMS value of the n-th harmonic of the rectifier, here the total harmonic distortion $T H D = \sqrt{\sum_{} \frac{1}{n^{2}} {|\frac{1}{1 - {(2 πf)}^{2} L C}|}^{2}}$ .

Here below you can see capacitive-input DC rectifier.

Here $V_{S} = V_{m} \sin ω t$ . $R_{i s}$ resistor used to limit the input-surge current when the rectifier is connected to power supply. When the voltage $V_{s}$ is higher than voltage $V_{L}$ , diodes $D_{1}$ and $D_{2}$ conducts, capacitor $C$ is charging. When the voltage of secondary winding $V_{s}$ of transformer is lower than $V_{L}$ , diodes $D_{1}$ and $D_{2}$ reverse biased, capacitor $C$ is discharged. The average value of capacitor voltage $V_{m} - V_{r (p p)} < V_{L} < V_{m}$ , $V_{r (p p)}$ is peak-to-peak ripple voltage $V_{r (p p)} = \frac{V_{m}}{f R C}$ .