What is a single-phase full-wave rectifier

Single-phase full-wave diode rectifier

Single-phase diode rectifier, converting ac signal into a dc voltage, exist in two types – half-wave and full-wave one. Half-wave diode rectifier was mentioned before.

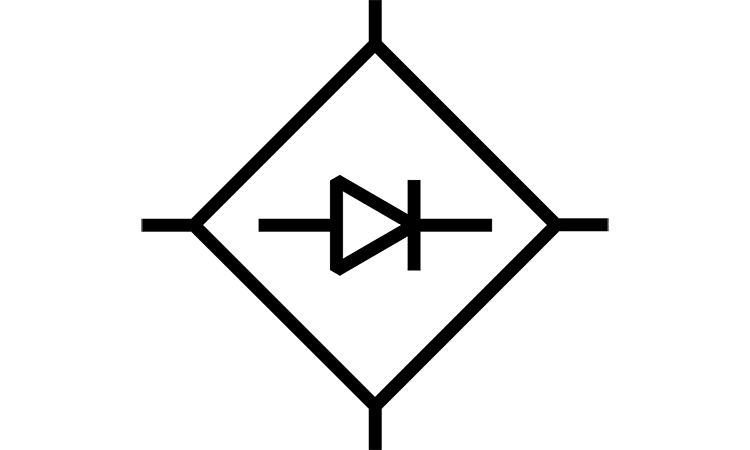
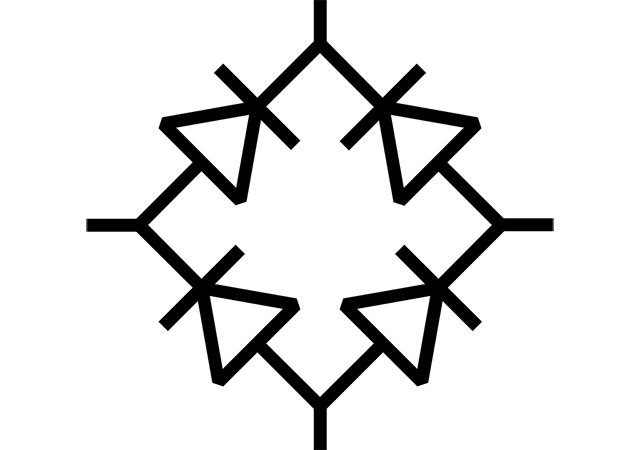
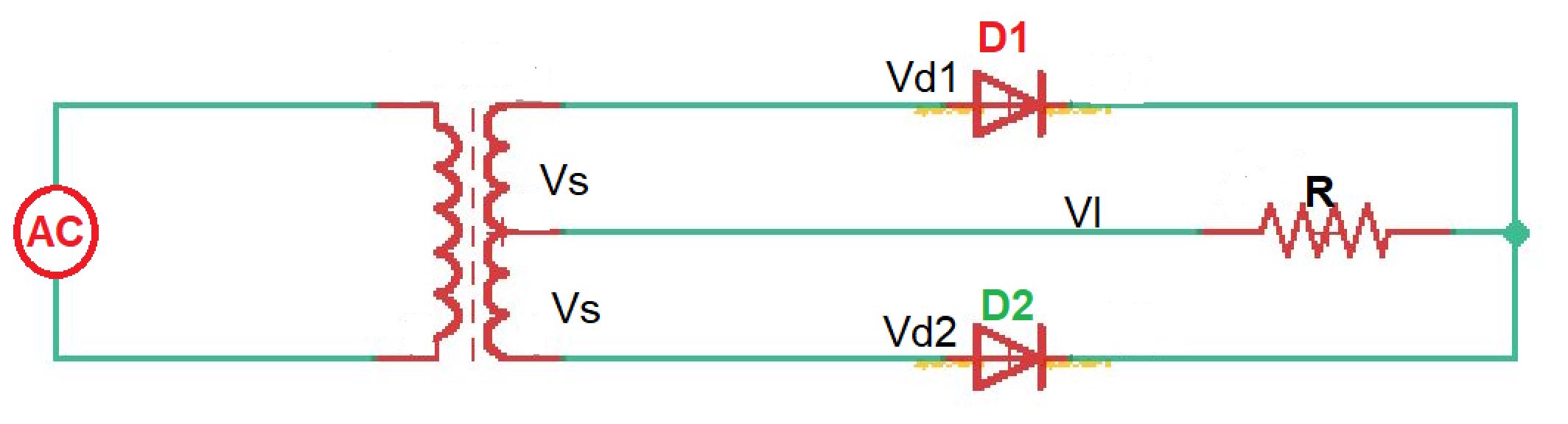
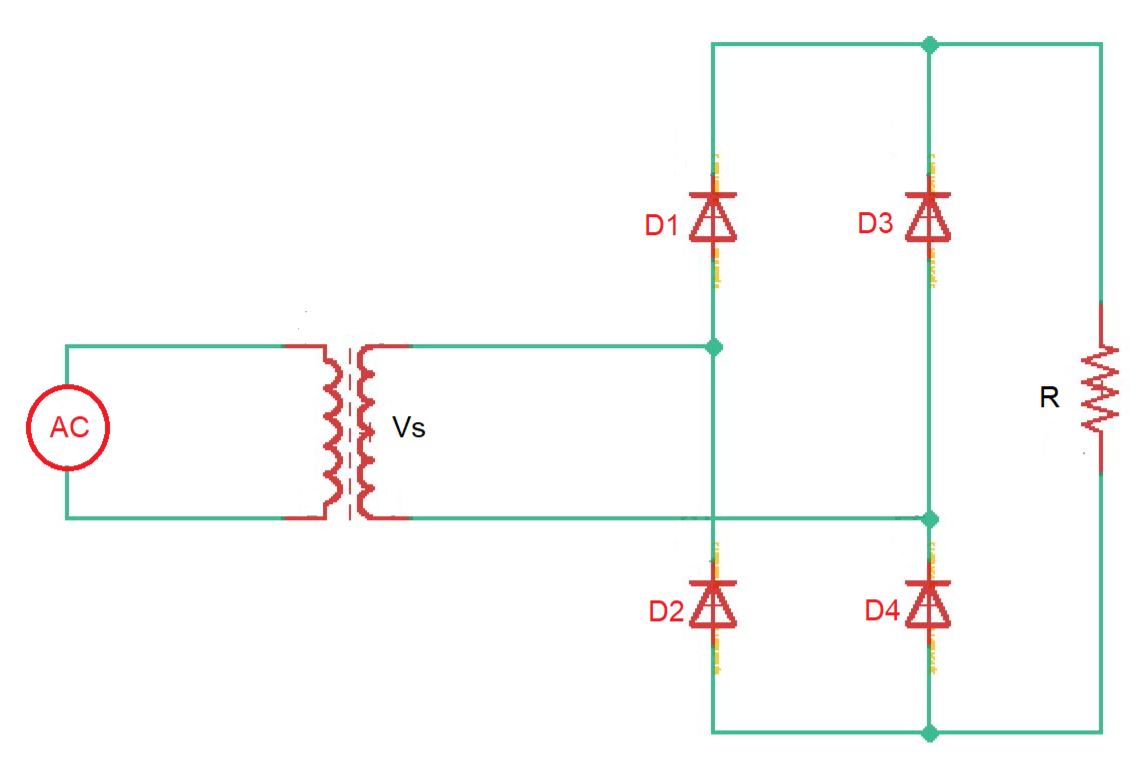
Full-wave diode rectifier can be two types as well – with a centre-tapped transformer and bridge rectifier. Both of them are depicted on the figure below.

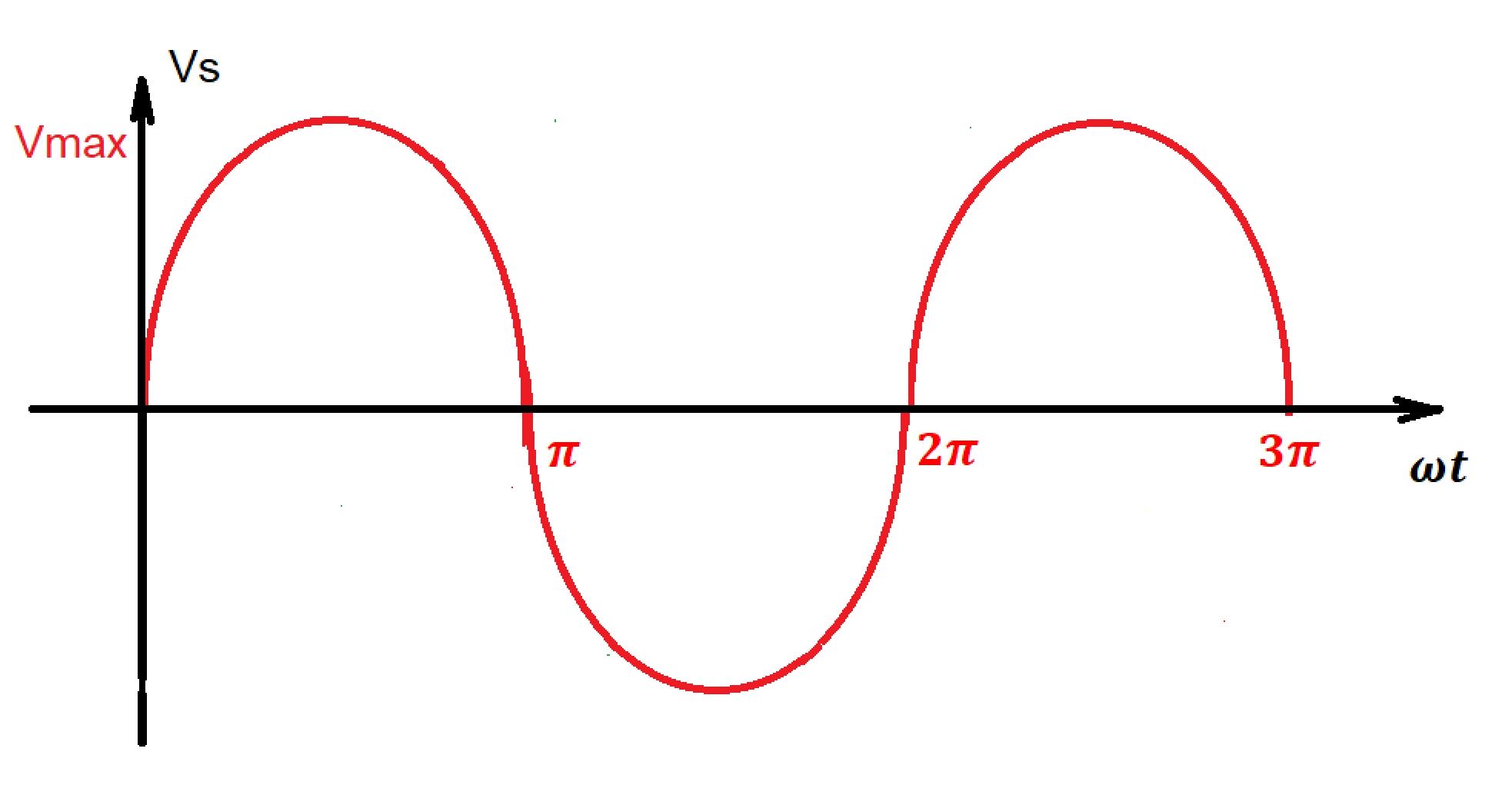
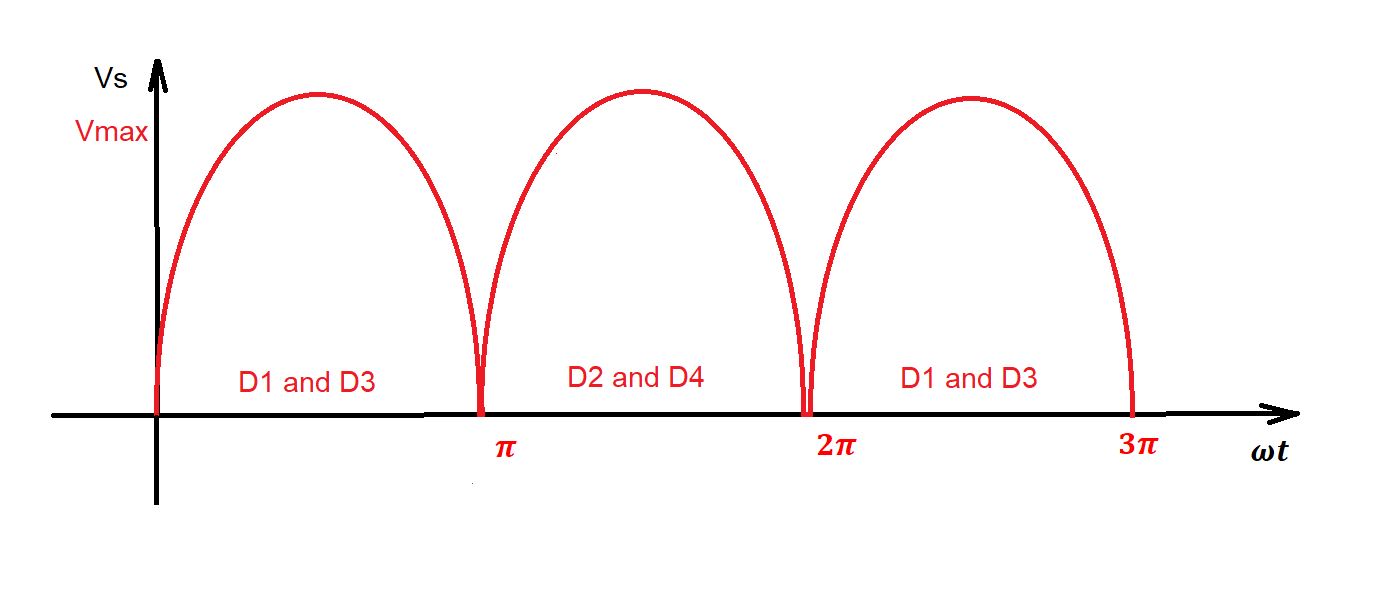
In the case of center-tapped transformer, we have two half-wave rectifiers, combined. The DC currents of these half-wave transformers are equal but opposite. Each diode conducts in corresponding half-cycle of transformer. Below you can see the current and voltage wave-forms for this rectifier.

full-wave centre-tapped rectifier — Full-wave center-tapped rectifier

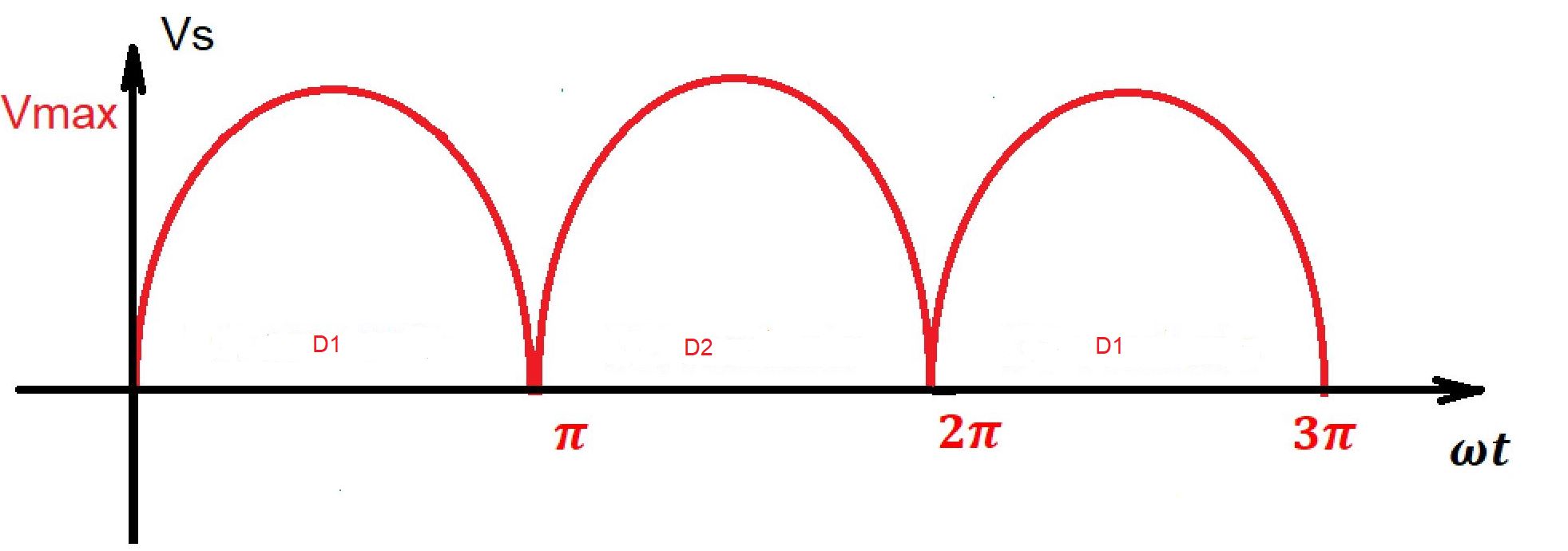
Bridge rectifier circuit is depicted below. Here we have four diodes instead of two. So in each half-cycle of transformer we have two conducting diodes. Below you can see voltage and current wave-forms for this rectifier.

full-wave bridge rectifier — Full-wave bridge rectifier

The average voltage is $V_{D C} = \frac{ω}{T} \int_{0}^{T} V_{m} \sin ω t d t$ .

So $V_{D C} = \frac{2 V_{m}}{π} = 0.636 V_{m}$ . Root-mean-square (RMS) value is $R M S = \sqrt{\frac{1}{T} \int_{0}^{T} {v^{2}}_{L} (t) d t} = \sqrt{\sqrt{\frac{ω}{π} \int_{0}^{π} {(V_{m} \sin ω t)}^{2} d t}}$

and $V_{L} = \frac{V_{m}}{\sqrt{2}} = 0.707 V_{m}$ .

The average value of load current $I_{d c} = \frac{V_{d c}}{R} = \frac{0.636 V_{d c}}{R}$ . And the RMS value of load current is $I_{L} = \frac{0.707 V_{m}}{R}$ .

The rectification ratio (RF), measures of rectification effectiveness $σ = \frac{P_{d c}}{P_{L}} = 0.81$ .

Form factor (FF) is a ratio of root-mean-square value of voltage or current to it’s average value. $F F = \frac{V_{L}}{V_{d c}}$ and $F F = \frac{I_{L}}{I_{d c}}$ . For full-wave rectifier $F F = 1.1$ .

Ripple factor (RF) is the measure of ripple $R F = \frac{V_{a c}}{V_{d c}}$ , where $V_{a c} = \sqrt{{V^{2}}_{L} + {V^{2}}_{d c}}$ . Making several mathematical simplifications $R F = \sqrt{{(\frac{V_{L}}{V_{d c}})}^{2} - 1} = \sqrt{F F^{2} - 1} = 0.482$ .

Transformer utilisation factor (TUF) is a transformer merit measure $T U M = \frac{V_{d c} I_{d c}}{V_{S} I_{S}}$ where $V_{S}$ and $I_{S}$ are rms voltage and rms current ratings of secondary transformer. Where for full-wave transformer $I_{S} = \frac{0.707 V_{m}}{R}$ .