Definition of complex number
A Complex number is a pair of real numbers (x;y). Its algebraic form is z=x+i*y, where i is an imaginary number. Its algebraic form is , where is an imaginary number. I – is a formal symbol, corresponding to the following equability i2 = -1.
Two complex numbers (x1;y1) and (x2;y2) are equal, when x1 = x2,y1 = y2 .
The sum of the complex numbers (x1;y1) and (x2;y2) is a complex number (x1 + x2; y1 + y2).
The product of complex numbers (x1;y1) and (x2;y2) is a complex number (x1x2 – y1y2; x1y2 + x2y1).
Complex numbers have the following features:
The Residual of complex numbers and is a complex number z + z2 = z1. The residual of complex numbers is z1 = x1 + i * y1 and z2 = x2 + i * y2 always exist and is defined by the formula:
Complex numbers z and are complex conjugated if . Module or absolute value of the complex number z=x+i*y is a real number .
Quotient of two complex numbers z1 and z2, (z2≠0), z, where z*z2=z1. If
The absolute value of the complex number states that: , then .
The real part of a complex number is: z=x+i*y, is x=Re(z).
The imaginary part of a complex number is: z=x+i*y, is y=Im(z).
Where .
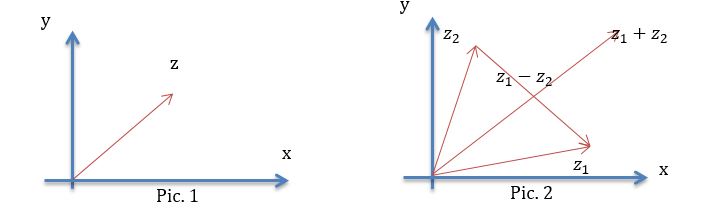
The Complex plane is a plane for representing complex numbers. X axis is a real axis, Y axis is an imaginary axis. As far as complex numbers are concerned z1,z2 and z3 correspond to the points on the complex plane so we can assume they are the same.
Definitions of sum and residual complex numbers mean that complex numbers sum up and subtract as vectors. Vector interpretation of sum and residual complex numbers are represented in Picture 2.
Let’s look at the triangle with the peaks 0, z1 and z1 + z2. The length of the triangle sides are .
Let’s look at the following sum:
Important corollary
Trigonometric form of a complex number , is the following:
where φ is an argument of the z number, and is described by the statements . Angle φ always exists, because . The argument of a complex number 0 does not exist.
All possible arguments are , where k is an integer. Usually φ=Arg z belongs to the angle range (-π;π).
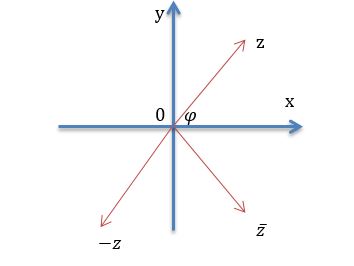
When z=x+iy, the arg z can be found from the following equalities:
Complex numbers z1 = z2 are equal, when .
The formula of multiplication and division of complex numbers is the following:
It means that when we multiply complex numbers their modules multiply and arguments sum up; when divided, the modules divide, and arguments subtract.
When .
When n belongs to the range of natural numbers,
Then the Moivre’s formula states:
, where m is an element of M unity.
Theorem. Equation zn = w, has n different complex roots , n belongs to N range.
Averment. Let’s suggest w=|w|*(cosθ+i sinθ). Then the complex number z should be:
z=|z|*(cosζ+i sinζ)
Let’s use an equation zn = w and Moivre’s formula:
The where k belongs to unity Z. With k=0,1,2,…,n-1 there are different root values. When k=n, root value is equal to the one with k=0. When k=n+1, the root value is equal to one with k=1 etc.
So the number of different root values is n, and
, where k=0,1,2,…n-1.
All n of zk roots belong to the circle with the radius , with the centre 0. They divide the circle by n parts with the angle .




