Mathematics Fundamentals: Complex numbers 2

Let’s suggest a function y=f(x) that is defined on the interval (a,b). Choose a point x on the interval (a,b), and another point x+∆x of this interval. ∆x is an increment of the function argument at the point x.

∆y=f(x+∆x)-f(x)

When x is fixed, ∆y is a function of ∆x. This is an increment of function y=f(x), in the point x.

$\frac{∆ y}{∆ x} = \frac{f (x +∆ x)- f (x)}{∆ x}$

The equation above is also a function of ∆x.

The derivative of a function =f(x) in the point x in the following limit: $\lim_{∆ x \to0} \frac{∆ y}{∆ x}$ .

In mathematics derivative marks f'(x) or y'(x).
In physics the following derivative uses: y ̇(x) or $\frac{dy}{dx}$ .

Derivative of some functions:
1. Function of a constant y=c, where c is a number.

∆y=f(x+∆x)-f(x)=c-c=0

$\lim_{∆ x \to0} {(\begin{matrix} ∆ y \\ ∆ x \end{matrix})}^{1} =0, c ‘=0$

2. Power function $y = x^{n}$ , n belongs to a real numbers unity. Then, $∆ y = f (x +∆ x)- f (x)=(x +∆ x)^{n} - x^{n} = x^{n} + {nx}^{n -1} ∆ x + n (n -1) x^{(n -2)} \frac{(∆ x)^{2}}{2} + \dots+(∆ x)^{n} - x^{n} = {nx}^{n -1} ∆ x + o (x), when ∆ x \overset{∆}{\to} 0, \frac{∆ y}{∆ x} = {nx}^{n -1} + \frac{o (∆ x)}{∆ x} \overset{∆}{\to} {nx}^{n -1}, where ∆ x \overset{∆}{\to} 0, then (x^{n})’= {nx}^{n -1}, where n belongs to the natural number s unity$

3. $y = \sin x ∆ y = \sin (x +∆ x)- \sin x =2 \sin \frac{∆ x}{2} * \cos (x + \frac{∆ x}{2}) = 2 (\frac{∆ x}{2} + o (x)* \cos (x + \frac{∆ x}{2}), ∆ x \overset{∆}{\to} 0 \frac{∆ y}{∆ x} =(1+ \frac{o (x)}{∆ x} * \cos (x + \frac{∆ x}{2}), ∆ x \overset{∆}{\to} 0 Finally (\sin x)’= \cos x .$

One-sided derivatives

\frac{∆ y}{∆ x} = \frac{f (x +∆ x)- f (x)}{∆ x},∆ x >0

If $\lim_{∆ x \to+0} (\frac{∆ y}{∆ x})^{1}$ exists, it names the right derivative of the function y=f(x) in the point x. It’s mark is $f_{r} ‘ (x).$

In the same way the left derivative of function is y=f(x) in the point x is: $\lim_{∆ x \to-0} (\frac{∆ y}{∆ x})^{1} = f_{l} ‘ (x)$ .

Let us look at the function y=|x|. In the x=0 we have:

$∆ y = y (0 + ∆ x) - y (0) = \{\begin{cases} ∆ x, ∆ x > 0 \\ - ∆ x, ∆ x < 0 \end{cases}, t h e r e f o r e \frac{∆ y}{∆ x} = \{\begin{cases} + 1, ∆ x > 0 \\ - 1, ∆ x < 0 \end{cases}$

Partial derivatives

Let us discuss the function z=f(x;y), the function of two variables x and y. If we fix for example, variable y, then we have the function f of one variable x. The Derivative of z=f(x;y) by variable is called partial derivative, and marks z_x^’. In the same way partial derivative z_y^’ is defined by the variable y.

Physical and geometrical meaning of derivatives. Physical meaning of derivative

Assume that x is time, and y=f(x) is the coordinate of a point on the X0Y plane at the moment of time x.

$\frac{∆ y}{∆ x} = \frac{f (x +∆ x)- f (x)}{∆ x}$ . is an average velocity of this point during a period of time from x till ∆x.
The magnitude $\lim_{∆ x \to0} \frac{∆ y}{∆ x} = f ‘ (x)= v (x)$ is an instaneous velocity of a part on the moment of time x.
In case of a random function y=f(x), its derivative f’ (x) is the velocity of change of variable y corresponding to change of variable x.

Geometric meaning of derivatives

Let’s assume the string l at the X0Y coordinate system. To align the 0X axis of a coordinate system with string l we have to turn it to the angle

- \frac{π}{2} < α < \frac{π}{2}

. The k=tan⁡ α is the slope of the string l in the coordinate system X0Y.

Let’s take a function y=f(x), where the unity of points ((f(x);x),x∈X) where X is a unity of points on this line. Let’s put points M(x,f(x)) and N(x+∆x,f(x+∆x)) on the line. The string MN is a secant in relation to the function on the graph. The angle φ(∆x) between the secant MN and 0X axis. Let’s suggest $∆ x \overset{∆}{\to} 0$ .

Then ∆y=f(x+∆x)-f(x).

If $\lim_{∆ x \to0} φ (Δx) = φ_{0}$ , so line l with slope k=tan⁡ $φ_{0}$ , which goes through the point M(x,f(x)) is a tangent to the function y=f(x) in the M point.
Also line l is a critical position of the secant MN, with $∆ x \overset{∆}{\to} 0$ . So we can say that the tangent to the function f(x) in the point M(x,f(x)) is a critical position of its secant MN, when $∆ x \overset{∆}{\to} 0$ .

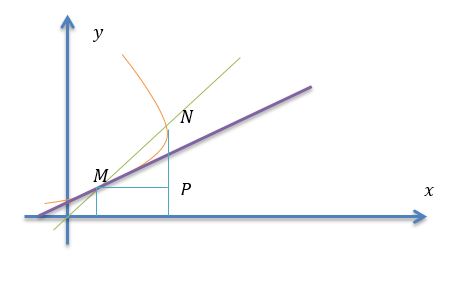
Theorem 1
If function y=f(x) has a derivative f'(x) in the point x, so y=f(x) has a tangent in the point M(x,f(x)), and its slope is equal to f'(x).

Proof
Let’s have a look on the MNP triangle:

$\tan φ (Δx)= \frac{∆ y}{∆ x}$ , in this way $φ (∆ x)= \tan^{-1} \frac{∆ y}{∆ x}$ .

$\lim_{∆ x \to0} \frac{∆ y}{∆ x} = f ‘ (x)$ , additionally $\tan^{-1} t$ is an incontinuous function.

$\lim_{∆ x \to0} φ (∆ x)= \lim_{∆ x \to0} \tan^{-1} \frac{∆ y}{∆ x} = \tan^{-1} f ‘ (x). Here φ_{0} = \lim_{∆ x \to0} φ (∆ x)= \tan^{-1} f ‘ (x) .$

By the tangence definition, tangence to the graph exists in the point M(x,f(x)).
And hence, $k = \tan φ_{0} = f ‘ (x)$ .

Tangence equation to the y=f(x), in the point $M (x_{0}, f (x_{0}))$ has the following form: $y - f (x_{0})= f ‘ (x_{0})(x - x_{0}).$

Differentiability, differential of a function and integral

Leave a Reply Cancel reply