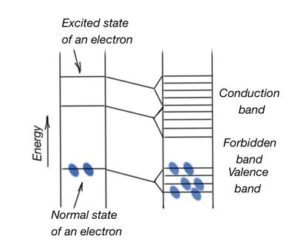
Energy band theory is a basis for describing processes and effects in solid crystals under electromagnetic field impact. Energy band theory is a theory of a valence electron moving in a periodic potential field of a crystalline lattice. Single atoms have a discrete energy spectrum, which means they can occupy only discrete energy levels. Part of these energy levels are filled with electrons in a non-excited condition. Part of these levels can be occupied only when electrons are excited. Atoms emit a quantity of energy during transition from excited levels to the levels with minimum of energy. Figure 6 shows the scheme of energy levels in the solid. For a system of the same atoms, the distanced is far enough away from each other, interaction is absent between them, and electron energy levels stay the same.
Interchangable interaction
When a compound has several phase transitions, all electron levels of all the atoms are shifting around each other, because of adjacent atoms interaction. Attraction between atom nucleus and electrons of adjacent atoms reduce the potential barrier, separating electrons of the adjacent atoms. During atoms convergence, their electron orbits are overlapping, and electrons can easily move from one atom to another without changing energy level. This is the easiest way for electrons to move across the crystal. Interchangable interaction have a quantum nature and is a consequence of the fact that electrons are indistinguishable. In this case we can’t say that a given electron belongs to the atom, it belongs to all atoms of a crystalline lattice.
Energy bands in solids
Discrete energy levels of an atom split into energy zones, because of interchangeable interaction. (Figure 6). Allowed energy bands are separated by forbidden energy intervals. Width of forbidden energy bands depend on nature of atoms, and crystalline lattice symmetry. Energy levels of internal orbits are closer to nucleus splitting than the levels of valence electrons. Both stationary and excited energy levels are splitting to the energy band. Width of the allowed energy bands increase with growing energy, and width of forbidden energy zones decrease. Each zone consists of a set of energy levels. Its quantity depends on the solid compound atom quantity. It means that in some abstract crystal, energy levels are distanced from each other on the distance inversely proportional to the quantity of atoms.
There are 1022 – 1023 atoms in a volume unit. Experimentally detected energetic length of valence electrons band is less the 1eV. It means that energy levels in a band are distanced from each other on 10-22 – 10-23eV. Very small energy impact is enough to provoke electron transition from one energy level to another.
Electrons distribution
Each energy level can contain only two electrons with different spin magnetic moment, in accordance to the Pauli principal. It means there is limited quantity of electronic states in a band, equal to the quantity of atomic states. There is also a limited quantity of electrons in the energy band. This fact plays an important role in crystal energy spectrum formation. Energy bands can be fully occupied, partially occupied and free. The most outer orbit occupied with electrons is called valence orbit. This energy band corresponds to the outer orbit of the atom. The adjacent free of electrons orbit is called the conductivity band. Mutual orientation of these two bands consider all the processes in a solid.
Band theory abstract
Energy spectra of conductors, semiconductors and insulators are very different. In conductors or metals, valence band is not fully occupied with electrons or partially overlap each other. For semiconductors and insulators, valence band and conduction band are derived by forbidden band. Tentatively semiconductors are those where forbidden band is less then 3eV, compounds with wider forbidden band are insulators. Real insulators may have 10eV forbidden band. The difference in the energy bands for conductors, semiconductors and insulators are shown in Figure 7.
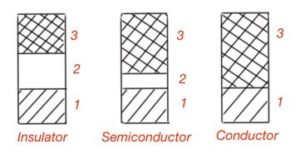
semiconductor and conductor
In accordance to the band theory, valence band electrons have the same movement freedom for all conductors, semiconductors and insulators. Electrons move by the tunnel transition from atom to atom. Valence bands of conductors, semiconductors and insulators behave differently in the external electromagnet field. External electromagnetic fields tend to break the symmetry of electrons in distribution by rate. Electrons are accelerating in the direction of the field and decelerating particles with the opposite impulse sign.
Any changes of the electron rate leads to a change in their energy, and electrons change their quantum states. Electron transition can happen if there is a free state in the valence band. Average additional energy electrons obtained in the electromagnet field is about 10-3 – 10-4eV, what is far more than the distance between energy sublevels in the band. In metals where valence band is not completely filled with electrons, even a small change of electron energy can transfer them to the adjacent free energy levels. That’s the reason why metals are good conductors.
In semiconductors and insulators all the electrons are in the valence band in temperature 0K. Conduction band is empty. Electrons from occupied valence levels can not go to the conduction band. To make an electron current we have to move some electrons from the valence band to the conduction band. Electromagnetic field energy is not enough to do such a transition. However, heating of a solid compound can work here.
The average kinetic energy of an atom heating oscillation is about:
There is always some part of an atom with bigger kinetic energy then average. Atoms can give their kinetic energy to some electrons, and these electrons will transfer from the valence band to the conduction band. The higher temperature and the smaller forbidden band, then interband transitions happen more frequently.
In each act of excitation and transition of electrons to the conduction band, there is an energy vacancy left in the valence band. These energy vacancies are called holes. Electrons can make transitions from level to level when there are holes in valence band (valence holes). Holes move in the opposite direction to the electron in the electromagnetic field. A hole behaves like a positive charge with negative effective mass.
The process of electrons make a transition to the free state accompanied with the inverse process – some electrons return to the normal state. It means there is a dynamic equilibrium in the compound – the quantity of electrons move to the conduction band equal to the quantity of electrons moved back in the valence band. The quantity of free electrons increases when the temperature is going up in the semiconductor, and decreases when the temperature is going down. It means a compound can be an insulator with one temperature, and becomes a semiconductor or conductor with another temperatures.
Electrons of the conduction band can not be absolutely free. They inevitably interact with the compound lattice. Periodic potential field of the lattice influences the electrons. To describe electron behaviour in the conductance band, its convenient to use the term of effective mass m0. Effective mass takes into account the complex character of interaction of electrons with the lattice, and it differs from the real mass of the electron. Density of the electron states in the band:
The forbidden band width changes with temperature.
- Amplitude of heating oscillations of the lattice atoms changes;
- Intersitial distances changes.
When the temperature goes up, the amplitude of heating oscillations of the atoms grows, and the rate of atom interaction and energy level splitting also grows. When the width of permitted level grows, the width of forbidden levels decreases.
The energy to transferring an electron into a free state and creating a hole, can be sourced not only from the heating energy of atomic oscillations, but also the energy of light absorption, electric and magnetic field energy and others. The growth of the quantity of free electrons or holes with any type of energy, enhances the compound conductance, current and electromotive force.
Electrical properties are considered by lattice atoms interaction and distances between them, but not the feature of the compound.
Impurities and point defects generate additional energy levels in the forbidden band of an ideal crystal. If impurities in atoms and defects are quite far from each other, interaction between them is absent, and correspondence to those energy levels is discrete. If the impurity atoms and defects are quite close to each other, their valence orbits can overlap, and discrete impurity energy levels split to the impurity energy bands. And this factor can enable conductance, if not all the levels in the band are occupied.
In conclusion, electrical properties of all the solid compounds are considered by excitation energy of charge careers. Good metals and good insulators are the very least examples of solid state materials. Solid band theory is applicable only for solids with covalent and metal bonds.