This post answers the question “What is definition of wireless network?”. The most important part in understanding how wireless technologies work is the fact that electromagnetic waves are carrying information.
Let’s imagine that there is a current flow through the conductor, and it is inducing the potential in other locations. The relationship between induced potential and currents is , here .
The multiplexing process is the sharing of the communication channel between multiple users.
Frequency division multiplexing is when the system can receive signals with certain periodicity and shape.
Spatial multiplexing – when the system limits signals to a specific geographical area.
Time-division multiplexing – the system limiting signals in accordance to specific time slots.
Directional multiplexing – the system accepting signals arriving from a specific angle.
Code division multiplexing – the system listens to the signals multiplied by a specific pattern.
Modern communication systems can combine and simultaneously use these multiplexing techniques. The core multiplexing technique is frequency-division multiplexing with certain frequency bands. The formula for this process is described several times at in the signals and systems section: , where is the signal we are multiplexing, and is a frequency we’d like to extract within a period of time .
Every signal can be represented from the frequency domain, or from the time domain. And every time-periodic signal can be presented as a set of sinus functions.
Filtering is the extracting of certain frequencies from complex signal.
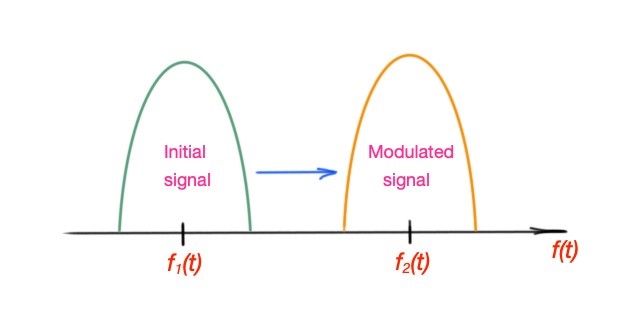
In order for the signal to transmit data it should be modulated. Modulation can be represented as .
When we perform frequency modulation, we are inevitably receiving components with different frequencies. The data containing signals have certain bandwidth around the nominal career frequency. Frequency modulation is schematically depicted in below.
Signal modulation.
One type of signal modulation is amplitude-shift keying (ASK), so in order to transmit more data, we must add amplitudes. The more information we want to transmit, the more amplitudes we add. That leads to increasing of error margin.
The second type of signal modulation is binary phase-shift keying (BPSK). Here, signal phase is used to distinguish bits. The more information we want to transmit, we should add phase states. This action also increases error margin. This method is used in 802-11 type networks. QPSK transmits 2-bits per symbol, and is called quaternary phase-shift keying (QPSK). Further variations are 8PSK, 16PSK and so on.
The other type of signal modulation is quadrature-amplitude modulation (QAM). The important term we should know here is signal to noise ratio (S/N), as this is the ratio between the measure of error to measure of noise.
The review of summary career approaches is depicted in Table 1.
Table 1. Carrier approaches review (Credit: “Wireless Networking: Know it all”, Praphul Chandra, Daniel M. Dobkin, Dan Bensky)
| Modulation type | Bit/symbol | Error / Margin | |
| OOK | 1 | 0.5 | 0.5 |
| 4ASK | 2 | 1/6 | 0.17 |
| BPSK | 1 | 1 | 1 |
| QPSK | 2 | 1/ | 0.71 |
| 16QAM | 4 | /6 | 0.71 |
| 64QAM | 6 | /14 | 0.1 |
If the signal to noise ratio is divided by the number of bits in the symbol, we get a measure called signal per bit of data.
,here is the total noise, is the signal bandwidth or noise power. Effective bit time is the product of symbols time and .Energy per bit is the product of bit time and signal power () .
is the measure of signal energy available per bit of data.The ratio can be expressed with dB measurement units via the relationship .
Important parts for building wireless networks can be found at Digi-Key Electronics web-site.