Resistors in parallel. Current divider rule derivation

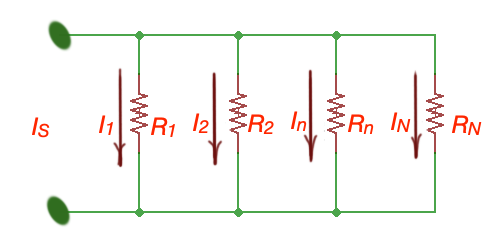
Two or more resistors are said to be in parallel, if identical voltage is across all the resistors.

In accordance to Kirhhoff’s Law the current $I_{S} = I_{1} + I_{2} + . . . + I_{N}$ , and $V_{1} = V_{2} = . . . = V_{N}$ $= V$ .

Here $I_{1} = \frac{V}{R_{1}}, I_{2} = \frac{V}{R_{2}}, . . . I_{N} = \frac{V}{R_{N}}$ . So $I_{S} = V (\frac{1}{R_{1}} + \frac{1}{R_{2}} + . . . \frac{1}{R_{N}}) = \frac{V}{R_{e q}}$ .

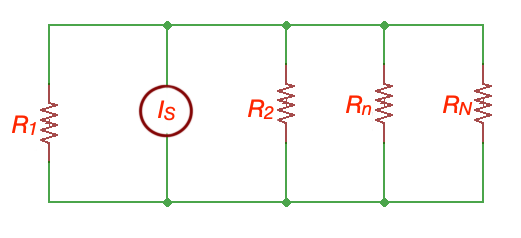
Here parallel resistors can be replaced by the equivalent resistance $\frac{1}{R_{e q}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + . . . \frac{1}{R_{N}}$ , and $R_{e q} = \frac{1}{\frac{1}{R_{1}} + \frac{1}{R_{2}} + . . . \frac{1}{R_{N}}}$ .

Then current through a resistor in parallel circuit is $I_{n} = \frac{\frac{1}{R_{n}}}{\frac{1}{R_{1}} + \frac{1}{R_{2}} + . . . \frac{1}{R_{N}}} I_{S}$ . This equation is called current divider. Current divider is a linear circuit, producing output current equal to a fraction of the input current.

For example, if $R_{1} = 1$ Ohm, $R_{2} = 2$ Ohm, $R_{3} = 4$ Ohm, $R_{4} = 2$ Ohm and $I_{s} = 4$ A, then $I_{3} = \frac{4}{9}$ A.