Magnetic circuit is a set of components, combined in one circuit, that create a magnetic field loop. In calculating magnetic circuits we must remember the laws of magnetic fields, discussed in a previous module. A magnetic circuit is symmetric if the magnetic flow through the branches is equal.
Branches of non-symmetric magnetic circuits have different magnetic flows. Magnetic circuits are characterised by the magnetic voltage in certain parts of a circuit described with the formula: , or .
Calculating magnetic circuits we can use Kirchhoff’s Laws. The first Kirchhoff Law states . The second Kirchhoff Law states . As we do with electric circuits, we can chose positive directions of magnetic flux, and positive loop directions. If magnetic flux has the same direction with the positive circuit loop, then magnetic voltage has a positive sign.
How to calculate parameters of magnetic component depicted below:
1. We have to calculate its measures for each part with constant cross-section.
2. Calculate the magnetic flux for each piece of magnetic component.
3. Calculate the magnetic field strength of each part.
4. Calculate the magnetic voltage for each part of the magnetic component.
To simplify the calculation we can think that the total magnetic flux is constant through the magnetic circuit. However, usually there is always some part of the flux that is scattered. Scattered magnetic flux is small for a small air gap in a magnetic structure. And the bigger the air gap the bigger the scattered magnetic flux.
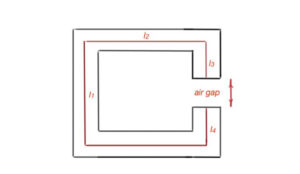 The example of geometry in the core of a magnetic circuit.
The example of geometry in the core of a magnetic circuit.