Explore the fundamentals of Norton’s Theorem and the concept of Norton Equivalent Circuit in electrical engineering.
Norton’s Theorem is a fundamental principle in electrical engineering that simplifies the analysis of complex circuits. This theorem states that any linear two-terminal circuit can be reduced to a simple equivalent circuit consisting of a single current source in parallel with a single resistor. This guide will explore Norton’s Theorem, the process of finding the Norton Equivalent Circuit, and its practical applications in circuit analysis.
Introduction to Norton’s Theorem
Named after Edward Lawry Norton, an engineer at Bell Labs, Norton’s Theorem offers a method for reducing a complex network into a simpler one for analysis purposes. Similar to Thévenin’s Theorem, which uses a voltage source and a series resistor, Norton’s approach focuses on a current perspective, which can be more intuitive in certain scenarios, especially in the analysis of parallel circuits.
Components of the Norton Equivalent Circuit
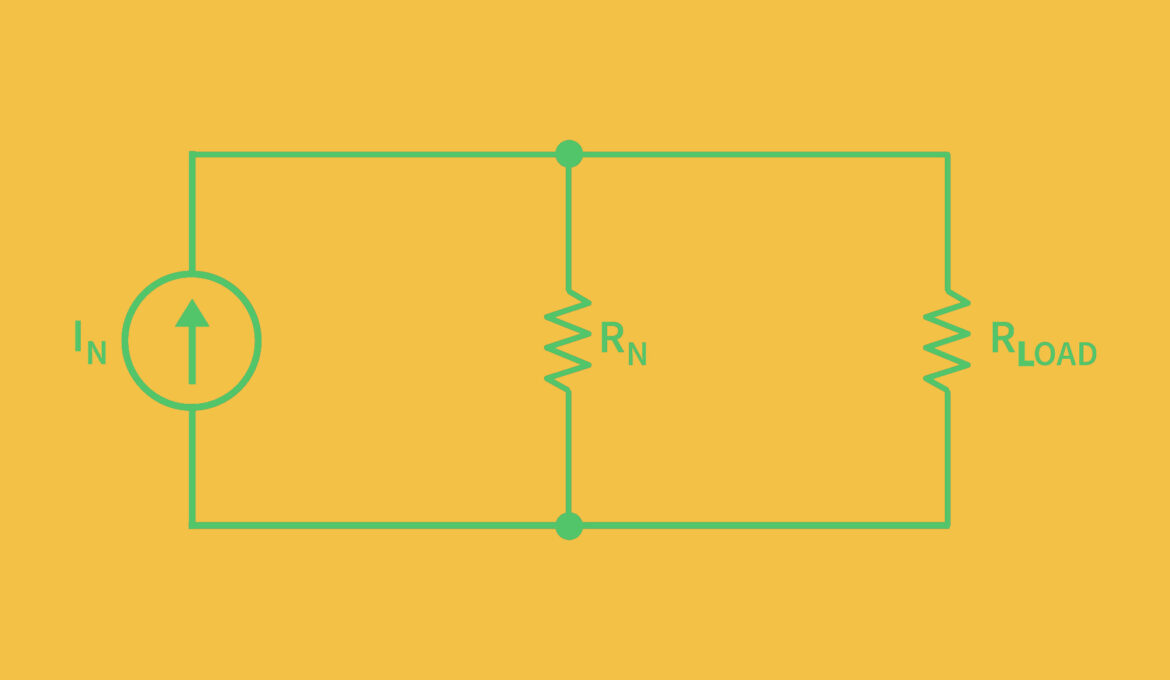
The Norton Equivalent Circuit comprises two parts:
- Norton Current (IN): This is the equivalent current source which represents the total current that would flow if the terminals were shorted together.
- Norton Resistance (RN): This is the resistance seen by the load if all the independent voltage sources were short-circuited and all independent current sources were opened. It is calculated in the same way as the Thévenin resistance.
Calculating the Norton Equivalent
The process to find the Norton Equivalent Circuit involves several steps:
- Remove the load: Detach the load resistor if present between the terminals of the circuit.
- Calculate RN: Replace all voltage sources with short circuits and all current sources with open circuits. Then, calculate the equivalent resistance across the terminals using series-parallel combinations or other methods such as mesh or nodal analysis.
- Calculate IN: With the load still removed, calculate the short-circuit current between the output terminals. This can be done using any standard circuit analysis technique like mesh or nodal analysis.
Example and application
Consider a circuit with a combination of resistors, a voltage source, and a current source. To find the Norton Equivalent:
- First, calculate the Norton Resistance (RN) by shorting the voltage sources and opening the current sources.
- Next, reattach the sources and calculate the short-circuit current (IN) flowing from one terminal to the other.
This equivalent circuit can then be used to analyse how the circuit will behave when connected to different loads, greatly simplifying complex network calculations.
Advantages of using Norton’s Theorem
- Simplification: It simplifies the analysis of complex circuits with multiple sources and components.
- Flexibility: It provides an alternative method for circuit analysis, complementing Thévenin’s Theorem.
- Practical applications: It is especially useful in power systems and communication circuits where parallel connections are predominant.
Conclusion
Norton’s Theorem is a powerful tool in the field of electrical engineering, enabling the simplification of complex networks into manageable forms. Understanding and applying Norton’s Theorem can significantly ease the analysis of electrical circuits, making it a critical concept for students and professionals in electrical engineering.
By mastering Norton’s Theorem, electrical engineering students can gain a deeper understanding of circuit functionality and enhance their ability to design and analyse complex networks effectively.